题目内容
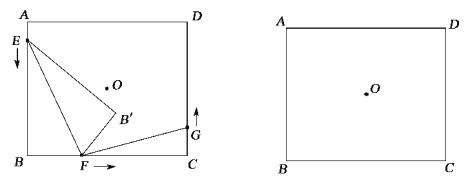
【题目】如图,点O为矩形ABCD的对称中心,AB=10cm,BC=12cm.点E,F,G分别从A,B,C三点同时出发,沿矩形的边按逆时针方向匀速运动,点E的运动速度为1cm/s,点F的运动速度为3cm/s,点G的运动速度为xcm/s.当点F到达点C(即点F与点C重合)时,三个点随之停止运动.在运动过程中,△EBF关于直线EF的对称图形是△EB'F,设点E,F,G运动的时间为t(单位:s).
(1)当t= s时,四边形EBFB'为正方形;
(2)当x为何值时,以点E,B,F为顶点的三角形与以点F,C,G为顶点的三角形可能全等?
(3)是否存在实数t,使得点B'与点O重合?若存在,求出t的值;若不存在,请说明理由.
【答案】(1)2.5;(2)3或4;(3)不存在,理由见解析
【解析】
(1)利用正方形的性质,得到BE=BF,列一元一次方程求解即可;
(2)分两种情况讨论,①△EBF≌△FCG,②△EBF≌△GCF,分别根据对应边相等列等式计算即可;
(3)本问为存在型问题.假设存在,则可以分别求出在同一条件下的t值,但它们互相矛盾,所以不存在.
解:(1)若四边形EBFB′为正方形,则BE=BF,BE=10-t,BF=3t,
即:10-t=3t,
解得t=2.5;
(2)分两种情况讨论:
①△EBF≌△FCG,
则EB=FC,BF=CG,
∴![]() ,
,
解得:![]() ,
,
②当△EBF≌△GCF时,
则EB=GC,BF=FC,
∴![]() ,
,
解得:![]() ,
,
综上,当x=3或4时,以点E,B,F为顶点的三角形与以点F,C,G为顶点的三角形可能全等;
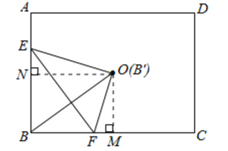
(3)假设存在实数t,使得点B′与点O重合.
如图,过点O作OM⊥BC于点M, ON⊥AB于点N,
则在Rt△OFM中![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
即![]() ,
,
解得:![]()
在Rt△OEN中,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
即![]() ,
,
解得:![]() ,
,
∵![]() ,
,
∴假设不成立,
即不存在实数t,使得点B'与点O重合.

 53天天练系列答案
53天天练系列答案




