题目内容
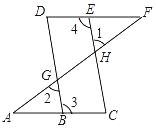
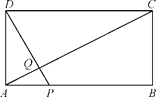
【题目】如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.
(1)求证:△APQ∽△CDQ;
(2)P点从A点出发沿AB边以每秒1个单位长度的速度向B点移动,移动时间为t秒.当t为何值时,DP⊥AC?
【答案】(1)见解析;(2)当t=5时,DP⊥AC,理由见解析
【解析】
(1)根据矩形的性质可得CD∥AB,根据平行线的性质可得∠DCQ=∠QAP,∠PDC=∠QPA,进而可得判定△APQ∽△CDQ;
(2)首先证明△ADQ∽△ACD,根据相似三角形的性质可得![]() ,然后计算出AC长,进而可得AQ长,再证明△AQP∽△ABC,可得
,然后计算出AC长,进而可得AQ长,再证明△AQP∽△ABC,可得![]() ,则
,则![]() ,再解即可得到t的值.
,再解即可得到t的值.
(1)证明:∵四边形ABCD是矩形,
∴CD∥AB,
∴∠DCQ=∠QAP,∠PDC=∠QPA,
∴△APQ∽△CDQ;
(2)解:当t=5时,DP⊥AC;
∵∠ADC=90°,DP⊥AC,
∴∠AQD=∠AQP=∠ADC=90°,
∵∠DAQ=∠CAD,
∴△ADQ∽△ACD,
∴![]() ,
,
AC=![]() ,
,
则AQ=![]() ,
,
∵∠AQP=∠ABC=90°,∠QAP=∠BAC,
∴△AQP∽△ABC,
∴![]() ,
,
则![]() ,
,
解得:t=5,
即当t=5时,DP⊥AC.

【题目】某社区准备五一组织社区内老年人去到县参加采摘节,现有甲、乙两家旅行社表示对老年人优惠,甲旅行社的优惠方式为:在原来每人100元的基础上,每人按照原价的60%收取费用;乙旅行社的优惠方式为:在收取一个600元固定团费的基础上,再额外收取每人40元.设参加采摘节的老年人有x人,甲、乙两家旅行社实际收费为![]() 元、
元、![]() 元.
元.
(Ⅰ)根据题意,填写下表:
老年人数量(人) | 5 | 10 | 20 | |
甲旅行社收费(元) | 300 | |||
乙旅行社收费)(元) | 800 |
(Ⅱ)求![]() 、
、![]() 关于x的函数关系式(不用写出自变量的取值范围)?
关于x的函数关系式(不用写出自变量的取值范围)?
(Ⅲ)如果![]() ,选择哪家旅行社合算?
,选择哪家旅行社合算?