题目内容
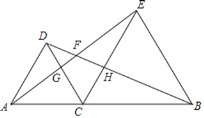
【题目】(1)操作与探究:如图,矩形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD的E点上,折痕的一端G点在边BC上,BG=10.
①第一次折叠:当折痕的另一端点F在AB边上时,如图1,求折痕GF的长;
②第二次折叠:当折痕的另一端点F在AD边上时,如图2,证明四边形BGEF为菱形,并求出折痕GF的长.

(2)拓展延伸:通过操作探究发现在矩形纸片ABCD中,AB=5,AD=13.如图3所示,折叠纸片,使点A落在BC边上的A′处,折痕为PQ.当点A′在BC边上移动时,折痕的端点P,Q也随之移动.若限定点P,Q分别在AB,AD边上移动,则点A′在BC边上可移动的最大距离是 .
【答案】(1)①GF=5![]() ;②4
;②4![]() ;(2)4.
;(2)4.
【解析】
(1)①首先利用翻折变换的性质以及勾股定理求出AE的长,进而利用勾股定理求出AF和EF的长,根据勾股定理即可得出结论;
②首先证明四边形BGEF是平行四边形,再利用BG=EG,得出四边形BGEF是菱形,再利用菱形性质求出FG的长;
(2)分别利用当点P与点B重合时,以及当点D与点Q重合时,求出A′B的极值进而得出答案.
(1)①解:如图①过G作GH⊥AD,
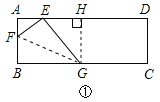
在Rt△GHE中,GE=BG=10,GH=8,
所以,EH=![]() =6,AE=10-6=4,
=6,AE=10-6=4,
设AF=x,则EF=BF=8-x,
则AF2+AE2=EF2,
∴x2+42=(8-x)2,
解得:x=3,
∴AF=3,BF=EF=5,
在Rt△BFG中,根据勾股定理得FG=![]() .
.
②证明:如图②,过F作FK⊥BG于K,

∵ABCD是矩形,
∴AD∥BC,BH∥EG,
∴四边形BGEF是平行四边形;
由对称性知,BG=EG,
∴四边形BGEF是菱形.
BG=BF=10,AB=8,AF=6,
∴KG=4,FG=![]() ;
;
(2)如图1,当点P与点B重合时,根据翻折对称性可得BA′=AB=5,
如图2,当点D与点Q重合时,根据翻折对称性可得
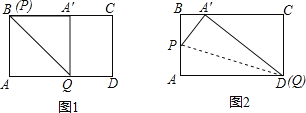
A′D=AD=13,
在Rt△A′CD中,A′D2=A′C2+CD2,
即132=(13-A′B)2+52,
解得:A′B=1,
所以点A'在BC上可移动的最大距离为5-1=4.

【题目】甲、乙两班各推选10名同学进行投篮比赛,按照比赛规则,每人各投了10个球,两个班选手的进球数统计如表,请根据表中数据解答下列问题
进球数/个 | 10 | 9 | 8 | 7 | 6 | 5 |
甲 | 1 | 1 | 1 | 4 | 0 | 3 |
乙 | 0 | 1 | 2 | 5 | 0 | 2 |
(1)分别写出甲、乙两班选手进球数的平均数、中位数与众数;
(2)如果要从这两个班中选出一个班级参加学校的投篮比赛,争取夺得总进球团体的第一名,你认为应该选择哪个班?如果要争取个人进球数进入学校前三名,你认为应该选择哪个班?