题目内容
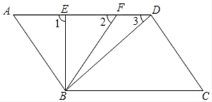
【题目】如图,点A是反比例函数y1= ![]() (x>0)图象上的任意一点,过点A作 AB∥x轴,交另一个比例函数y2=
(x>0)图象上的任意一点,过点A作 AB∥x轴,交另一个比例函数y2= ![]() (k<0,x<0)的图象于点B.
(k<0,x<0)的图象于点B.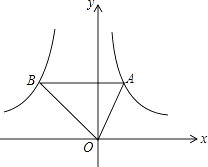
(1)若S△AOB的面积等于3,则k是=;
(2)当k=﹣8时,若点A的横坐标是1,求∠AOB的度数;
(3)若不论点A在何处,反比例函数y2= ![]() (k<0,x<0)图象上总存在一点D,使得四边形AOBD为平行四边形,求k的值.
(k<0,x<0)图象上总存在一点D,使得四边形AOBD为平行四边形,求k的值.
【答案】
(1)﹣4
(2)解:∵点A的横坐标是1,
∴y= ![]() =2,
=2,
∴点A(1,2),
∵AB∥x轴,
∴点B的纵坐标为2,
∴2=﹣ ![]() ,
,
解得:x=﹣4,
∴点B(﹣4,2),
∴AB=AC+BC=1+4=5,OA= ![]() =
= ![]() ,OB=
,OB= ![]() =2
=2 ![]() ,
,
∴OA2+OB2=AB2,
∴∠AOB=90°;
(3)解:假设y2= ![]() 上有一点D,使四边形AOBD为平行四边形,
上有一点D,使四边形AOBD为平行四边形,
过D作DE⊥AB,过A作AC⊥x轴,
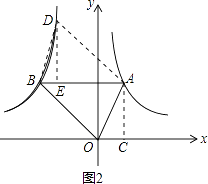
∵四边形AOBD为平行四边形,
∴BD=OA,BD∥OA,
∴∠DBA=∠OAB=∠AOC,
在△AOC和△DBE中,
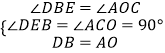 ,
,
∴△AOC≌△DBE(AAS),
设A(a, ![]() )(a>0),即OC=a,AC=
)(a>0),即OC=a,AC= ![]() ,
,
∴BE=OC=a,DE=AC= ![]() ,
,
∴D纵坐标为 ![]() ,B纵坐标为
,B纵坐标为 ![]() ,
,
∴D横坐标为 ![]() ,B横坐标为
,B横坐标为 ![]() ,
,
∴BE=| ![]() ﹣
﹣ ![]() |=a,即﹣
|=a,即﹣ ![]() =a,
=a,
∴k=﹣4.
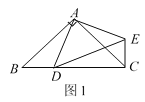
【解析】解:如图1,设AB交y轴于点C,
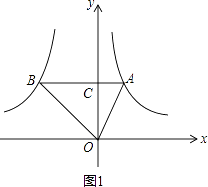
∵点A是反比例函数y1= ![]() (x>0)图象上的任意一点,且AB∥x轴,
(x>0)图象上的任意一点,且AB∥x轴,
∴AB⊥y轴,
∴S△AOC= ![]() ×2=1,
×2=1,
∵S△AOB=3,
∴S△BOC=2,
∴k=﹣4;
所以答案是:﹣4;
【考点精析】认真审题,首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2),还要掌握勾股定理的逆定理(如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形)的相关知识才是答题的关键.