题目内容
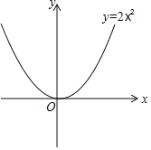
【题目】如图，在平面直角坐标系xOy中，对称轴为直线x=1的抛物线y=-x2+bx+c与x轴交于点A和点B，与y轴交于点C，且点B的坐标为（-1，0）
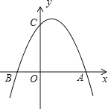
（1）求抛物线的解析式；
（2）点D的坐标为（0，1），点P是抛物线上的动点，若△PCD是以CD为底的等腰三角形，求点P的坐标．
【答案】（1）y=﹣x2+2x+3；（2）点P的坐标为（1+
，2）或（1﹣，2）．
【解析】
（1）求出A、B坐标，利用待定点C的坐标为（0，3），点D（1，0），
（2）由点C的坐标为（0，3），点D（1，0），可知满足条件的点P的纵坐标为2，解方程-x2+2x+3=2即可得到点P的横坐标，由此即可解决问题．
解：（1）∵抛物线的对称轴为直线x=1，y=﹣x2+bx+c与x轴交于点A和点B，
∴由题意可求点A的坐标为（3，0）．
将点A（3，0）和点B（﹣1，0）代入y=﹣x2+bx+c，
得 
，
解得 
，
∴抛物线的解析式y=﹣x2+2x+3．
（2）如图，
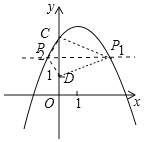
∵点C的坐标为（0，3），点D（1，0），
∴满足条件的点P的纵坐标为2．
∴﹣x2+2x+3=2．
解得 x1=1+，x2=1﹣，
∴点P的坐标为（1+，2）或（1﹣，2）．
全能测控期末小状元系列答案
【题目】探究函数
的图象与性质．
小娜根据学习函数的经验，对函数的图象与性质进行了探究．下面是小娜的探究过程，请补充完整：
（1）下表是x与y的几组对应值．
x | … |
|
| 0 |
| 2 |
| 3 | … |
y | … |
|
| 0 | m | n |
| 3 | … |
请直接写出：m= ，n= ；
（2）如图，小娜在平面直角坐标系xOy中，描出了上表中已经给出的各组对应值为坐标的点，请再描出剩下的两个点，并画出该函数的图象；
（3）结合画出的函数图象，解决问题：若方程
有三个不同的解，记为x1, x2, x3，且x1< x2<x3. 请直接写出x1+ x2+x3的取值范围.
【题目】有这样一个问题：探究函数y＝
的图象与性质.小美根据学习函数的经验，对函数y＝的图象与性质进行了探究下面是小美的探究过程，请补充完整：
(1)函数y＝的自变量x的取值范围是 ；
(2)下表是y与x的几组对应值.
x | －2 | － | －1 | － |
|
| 1 | 2 | 3 | 4 | … |
y | 0 | － | －1 | － |
|
|
| m |
|
| … |
求m的值；
(3)如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点.根据描出的点，画出该函数的图象；
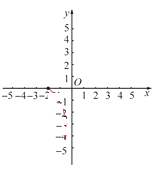
(4)结合函数的图象，写出该函数的一条性质： .
【题目】某市居民的交通消费可分为交通工具、交通工具使用燃料、交通工具维修、市内公共交通、城市间交通五项.该市统计局根据当年各项的权重及各项价格的涨幅，计算当年居民交通消费价格的平均涨幅.2017年该市的有关数据如下表所示.
交通工具 | 交通工具使用燃料 | 交通工具维修 | 市内公共交通 | 城市间交通 | |
占交通消费的比例 | 22% | 13% | 5% | P | 26% |
相对上一年价格的涨幅 | 1.5% | m% | 2% | 0.5% | 1% |
（1）求p的值；
（2）若2017年该市的居民交通消费相对上一年价格的平均涨幅为1.25%，求m的值.