题目内容
如图，半圆O的直径AB=4，与半圆内切的⊙O1与AB切于C，设AC=x，⊙O1的半径为y，则y与x的关系式为______．
连接O1C，O1O，如图所示：
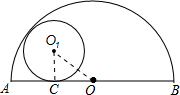
∵圆O1与AB相切与点C，且圆O1的半径为y，
∴O1C⊥AB，O1C=y，
∵AB=4，
∴OA=2，又AC=x，
∴OC=OA-AC=2-x，
∵圆O1与圆O内切，
∴圆心距d=OO1=2-y，
在Rt△O1CO中，根据勾股定理得：O1C2+CO2=O1O2，
即y2+（2-x）2=（2-y）2，
化简得：y=-
x2+x．
故答案为：y=-
x2+x
∵圆O1与AB相切与点C，且圆O1的半径为y，
∴O1C⊥AB，O1C=y，
∵AB=4，
∴OA=2，又AC=x，
∴OC=OA-AC=2-x，
∵圆O1与圆O内切，
∴圆心距d=OO1=2-y，
在Rt△O1CO中，根据勾股定理得：O1C2+CO2=O1O2，
即y2+（2-x）2=（2-y）2，
化简得：y=-
| 1 |
| 4 |
故答案为：y=-
| 1 |
| 4 |
练习册系列答案
名校课堂系列答案
相关题目
的关系式为r=1+t（t≥0），当点A出发后______秒两圆相切．
