题目内容
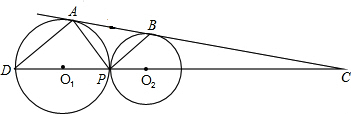
已知：如图，⊙O1与⊙O2外切于点P，AB为⊙O1、⊙O2的外公切线，切点分别为A、B，连心线O1O2分别交⊙O1于D、交AB于C，连接AD、AP、BP．求证：（1）AD∥BP；（2）CP•CO1=CD•CO2；（3）
=
．
| AD |
| AP |
| PC |
| BC |
证明：（1）过P作两圆的内公切线PE交AB于E，
∵EA、EP为⊙O1的切线，
∴EA=EP，
同理：EB=EP，
∴∠APB=90°，
∵PD是⊙O1的直径，
∴∠DAP=90°，
∴∠APB=∠DAP，
∴AD∥BP；
（2）由（1）知：AD∥BP?
=
，
连接O1A、O2B，AB分别切两圆于A、B，
∴
?O1A∥O2B?
=
，
∴
=
，
∴CP•CO1=CD•CO2；
（3）由（1）知：∠DAP=∠APB，
又AB是⊙O1的切线，AP是⊙O1的弦，
∴∠D=∠PAB，
∴△DAP∽△APB，
∴
=
，
又∵
?
=△CPA∽△CBP?
=
，
∴
=
．
∵EA、EP为⊙O1的切线，
∴EA=EP，
同理：EB=EP，
∴∠APB=90°，
∵PD是⊙O1的直径，
∴∠DAP=90°，
∴∠APB=∠DAP，
∴AD∥BP；
（2）由（1）知：AD∥BP?
| CP |
| CD |
| CB |
| CA |
连接O1A、O2B，AB分别切两圆于A、B，
∴
|
| CO2 |
| CO1 |
| CB |
| CA |
∴
| CP |
| CD |
| CO2 |
| CO1 |
∴CP•CO1=CD•CO2；
（3）由（1）知：∠DAP=∠APB，
又AB是⊙O1的切线，AP是⊙O1的弦，
∴∠D=∠PAB，
∴△DAP∽△APB，
∴
| AD |
| AP |
| AP |
| BP |
又∵
|
|
| AP |
| BP |
| PC |
| BC |
∴
| AD |
| AP |
| PC |
| BC |
练习册系列答案
名校课堂系列答案
相关题目
的关系式为r=1+t（t≥0），当点A出发后______秒两圆相切．