题目内容
【题目】如图:在平行四边形ABCD中,对角线AC与BD交于点O,过点O的直线EF分别与AD、BC交于点E、F,EF⊥AC,连结AF、CE.
(1)求证:OE=OF;
(2)请判断四边形AECF是什么特殊四边形,请证明你的结论.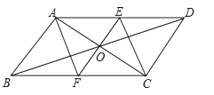
【答案】证明:(1)∵四边形ABCD平行四边形,
∴AD∥BC,OA=CO,
∴∠DAO=∠BCO,
在△AEO和△CFO中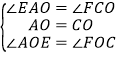 ,
,
∴△AEO≌△CFO(ASA),
∴OE=OF;
(2)答:四边形AECF是菱形,
∵△AEO≌△CFO,
∴AE=CF,
∵AE∥FC,
∴四边形AECF平行四边形,
∵EF⊥AC,
∴四边形AECF是菱形.
【解析】(1)首先根据平行四边形的性质可得AD∥BC,OA=CO,再证明△AEO≌△CFO可得OE=OF;
(2)根据△AEO≌△CFO可得AE=CF,然后可得四边形AECF平行四边形,再由条件EF⊥AC可得四边形AECF是菱形.

练习册系列答案
相关题目