题目内容
【题目】如图1,在△ABO中,∠OAB=90°,∠AOB=30°,OB=8.以OB为一边,在△OAB外作等边三角形OBC,D是OB的中点,连接AD并延长交OC于E. 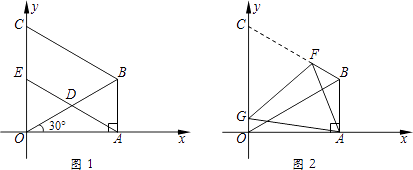
(1)求点B的坐标;
(2)求证:四边形ABCE是平行四边形;
(3)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.
【答案】
(1)解:在△OAB中,∠OAB=90°,∠AOB=30°,OB=8,
∴OA=OBcos30°=8× ![]() =4
=4 ![]() ,
,
AB=OBsin30°=8× ![]() =4,
=4,
∴点B的坐标为(4 ![]() ,4)
,4)
(2)证明:∵∠OAB=90°,
∴AB⊥x轴,
∵y轴⊥x轴,
∴AB∥y轴,即AB∥CE,
∵∠AOB=30°,
∴∠OBA=60°,
∵DB=DO=4
∴DB=AB=4
∴∠BDA=∠BAD=120°÷2=60°,
∴∠ADB=60°,
∵△OBC是等边三角形,
∴∠OBC=60°,
∴∠ADB=∠OBC,
即AD∥BC,
∴四边形ABCE是平行四边形
(3)解:设OG的长为x,
∵OC=OB=8,
∴CG=8﹣x,
由折叠的性质可得:AG=CG=8﹣x,
在Rt△AOG中,AG2=OG2+OA2,
即(8﹣x)2=x2+(4 ![]() )2,
)2,
解得:x=1,
即OG=1
【解析】(1)由在△ABO中,∠OAB=90°,∠AOB=30°,OB=8,根据三角函数的知识,即可求得AB与OA的长,即可求得点B的坐标;(2)首先可得CE∥AB,D是OB的中点,根据直角三角形斜边的中线等于斜边的一半,可证得BD=AD,∠ADB=60°,又由△OBC是等边三角形,可得∠ADB=∠OBC,根据内错角相等,两直线平行,可证得BC∥AE,继而可得四边形ABCD是平行四边形;(3)首先设OG的长为x,由折叠的性质可得:AG=CG=8﹣x,然后根据勾股定理可得方程(8﹣x)2=x2+(4 ![]() )2 , 解此方程即可求得OG的长.
)2 , 解此方程即可求得OG的长.