题目内容
【题目】如图,在ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF.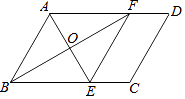
(1)求证:四边形ABEF是菱形;
(2)若AE=6,BF=8,CE= ![]() ,求ABCD的面积.
,求ABCD的面积.
【答案】
(1)
解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB,
∵∠BAD的平分线交BC于点E,
∴∠DAE=∠BEA,
∴∠BAE=∠BEA,
∴AB=BE,同理可得AB=AF,
∴AF=BE,
∴四边形ABEF是平行四边形,
∵AB=AF.
∴四边形ABEF是菱形
(2)
解:作FG⊥BC于G,
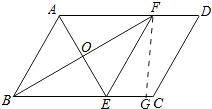
∵四边形ABEF是菱形,AE=6,BF=8,
∴AE⊥BF,OE= ![]() AE=3,OB=
AE=3,OB= ![]() BF=4,
BF=4,
∴BE= ![]() =5,
=5,
∵S菱形ABEF= ![]() AEBF=BEFG,
AEBF=BEFG,
∴GF= ![]() ,
,
∴S平行四边形ABCD=BCFG=(BE+EC)GF=(5+ ![]() )×
)× ![]() =36.
=36.
【解析】(1)先证明四边形ABEF是平行四边形,再证明邻边相等即可得出答案.(2)作FG⊥BC于点G,根据S菱形ABEF= ![]() AEBF=BEFG,先求出FG,再根据S平行四边形ABCD=BCFG,即可得出答案.
AEBF=BEFG,先求出FG,再根据S平行四边形ABCD=BCFG,即可得出答案.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.

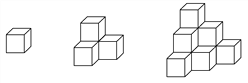
【题目】如图棱长为a的小正方体,按照下图的方法继续摆放,自上而下分别叫第一层、第二层…第n层,第n层的小正方体的个数记为S.解答下列问题:
n | 1 | 2 | 3 | 4 | … |
S | 1 | 3 | … |
(1)按要求填写上表:
(2)研究上表可以发现S随n的变化而变化,且S随n的增大而增大有一定的规律,请你用式子来表示S与n的关系,并计算当n=10时,S的值为多少?
【题目】八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个类型,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.
类别 | 频数(人数) | 频率 |
小说 | 0.5 | |
戏剧 | 4 | |
散文 | 10 | 0.25 |
其他 | 6 | |
合计 | 1 |
根据图表提供的信息,解答下列问题:
(1)八年级一班有多少名学生?
(2)请补全频数分布表,并求出扇形统计图中“其他”类所占的百分比;
(3)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从以上四位同学中任意选出2名同学参加学校的戏剧兴趣小组,请用画树状图或列表法的方法,求选取的2人恰好是乙和丙的概率.