题目内容
在平面直角坐标系xOy中,反比例函数 的图象与抛物线y=x2+(9m+4)x+m-
的图象与抛物线y=x2+(9m+4)x+m- 1交于点A(3,n).
1交于点A(3,n).
(1)求n的值及抛物线的解析式;
(2)过点A作直线BC,交x轴于点B,交反比例函数 (x>0)的图象于点C,且AC=2AB,求B、C两点的坐标;
(x>0)的图象于点C,且AC=2AB,求B、C两点的坐标;
(3)在(2)的条件下,若点P是抛物线对称轴上的一点,且点P到x轴和直线BC的距离相等,求点P的坐标.
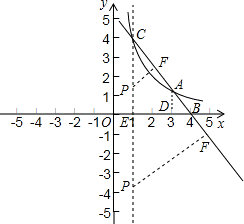 解:(1)∵点A(3,n)在反比例函数
解:(1)∵点A(3,n)在反比例函数 的图象上,
的图象上,∴n=
 ,
,∴A(3,
 ).
).∵点A(3,
 )在抛物线y=x2+(9m+4)x+m-1上,
)在抛物线y=x2+(9m+4)x+m-1上,∴
 =9+(9m+4)×3+m-1,
=9+(9m+4)×3+m-1,∴m=-
 .
.∴抛物线的解析式为y=x2-2x-
 ;
;(2)分别过点A、C作x轴的垂线,垂足分别为点D、E,
∴AD∥CE.
∴△ABD∽△CBE.
∴
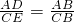 .
.∵AC=2AB,
∴
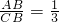 .
.由题意,得AD=
 ,
,∴
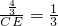 .
.∴CE=4.
即点C的纵坐标为4.
当y=4时,x=1,
∴C(1,4),
∵
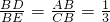 ,DE=2,
,DE=2,∴
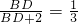 .
.∴BD=1.
∴B(4,0);
(3)∵抛物线
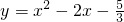 的对称轴是x=1,
的对称轴是x=1,∴P在直线CE上.
过点P作PF⊥BC于F.
由题意,得PF=PE.
∵∠PCF=∠BCE,∠CFP=∠CEB=90°,
∴△PCF∽△BCE.
∴
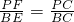 .
.由题意,得BE=3,BC=5.
①当点P在第一象限内时,设P(1,a)(a>0).
则有
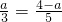 .解得
.解得 .
.∴点P的坐标为(1,
 ).
).②当点P在第四象限内时,设P(1,a)(a<0)
则有
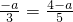 .解得a=-6.
.解得a=-6.∴点P的坐标为(1,-6).
∴点P的坐标为(1,
 )或(1,-6).
)或(1,-6).分析:(1)由点A(3,n)在反比例函数
 的图象上,即可求得n的值,又由点A在抛物线y=x2+(9m+4)x+m-1上,利用待定系数法即可求得;
的图象上,即可求得n的值,又由点A在抛物线y=x2+(9m+4)x+m-1上,利用待定系数法即可求得;(2)首先由AD∥CE,证得△ABD∽△CBE,根据相似三角形的对应边成比例,即可求得AD的长,则可求得CE的长,易得点C的坐标,即可求得点B的坐标;
(3)首先求得:抛物线
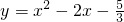 的对称轴,证得:△PCF∽△BCE,再分别从当点P在第一象限内时,设P(1,a)(a>0)与当点P在第四象限内时,设P(1,a)(a<0)利用相似三角形的对应边成比例求解即可.
的对称轴,证得:△PCF∽△BCE,再分别从当点P在第一象限内时,设P(1,a)(a>0)与当点P在第四象限内时,设P(1,a)(a<0)利用相似三角形的对应边成比例求解即可.点评:此题考查了待定系数法求二次函数的解析式以及相似三角形的判定与性质等知识.此题综合性很强,难度较大,注意数形结合思想与分类讨论思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
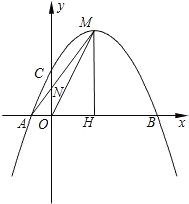 直线QG的解析式;若不存在,请说明理由.
直线QG的解析式;若不存在,请说明理由.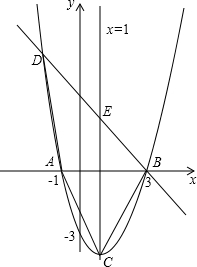 点B在A点的右侧;交y轴于(0,-3).
点B在A点的右侧;交y轴于(0,-3).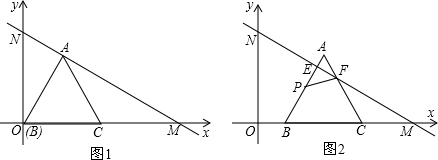
 ,对称轴l与x轴相交于点C,顶点为点D,且∠ADC的正切值为
,对称轴l与x轴相交于点C,顶点为点D,且∠ADC的正切值为 如图①,在等腰直角三角板ABC中,斜边BC为2个单位长度,现把这块三角板在平面直角坐标系xOy中滑动,并使B、C两点始终分别位于y轴、x轴的正半轴上,直角顶点A与原点O位于BC两侧.
如图①,在等腰直角三角板ABC中,斜边BC为2个单位长度,现把这块三角板在平面直角坐标系xOy中滑动,并使B、C两点始终分别位于y轴、x轴的正半轴上,直角顶点A与原点O位于BC两侧.