题目内容
(2012•卢湾区一模)如图,已知在平面直角坐标系xoy中,抛物线y=ax2+bx+c(a>0)与x轴相交于A(-1,0),B(3,0)两点 ,对称轴l与x轴相交于点C,顶点为点D,且∠ADC的正切值为
,对称轴l与x轴相交于点C,顶点为点D,且∠ADC的正切值为
.
(1)求顶点D的坐标;
(2)求抛物线的表达式;
(3)F点是抛物线上的一点,且位于第一象限,连接AF,若∠FAC=∠ADC,求F点的坐标.
 ,对称轴l与x轴相交于点C,顶点为点D,且∠ADC的正切值为
,对称轴l与x轴相交于点C,顶点为点D,且∠ADC的正切值为| 1 | 2 |
(1)求顶点D的坐标;
(2)求抛物线的表达式;
(3)F点是抛物线上的一点,且位于第一象限,连接AF,若∠FAC=∠ADC,求F点的坐标.
分析:(1)由抛物线和x轴交于A,B两点,可求出对称轴方程,再由已知条件可求出CD的长,进而求出D的坐标;
(2)设抛物线的解析式为y=a(x-h)2+k,由(1)可知h=1,k=-4,再把A或B点的坐标代入求出a的值即可;
(3)过点F作作FH⊥x轴,垂足为点H,设F(x,x2-2x-3),由已知条件求出x的值,即可求出F的坐标.
(2)设抛物线的解析式为y=a(x-h)2+k,由(1)可知h=1,k=-4,再把A或B点的坐标代入求出a的值即可;
(3)过点F作作FH⊥x轴,垂足为点H,设F(x,x2-2x-3),由已知条件求出x的值,即可求出F的坐标.
解答:解:(1)∵抛物线与x轴相交于A(-1,0),B(3,0)两点,
∴对称轴直线l=
=1,
∵对称轴l与x轴相交于点C,
∴AC=2,
∵∠ACD=90°,tan∠ADC=
,
∴CD=4,
∵a>0,
∴D(1,-4);
(2)设y=a(x-h)2+k,有(1)可知h=1,k=-4,
∴y=a(x-1)2-4,
将x=-1,y=0代入上式,
得:a=1,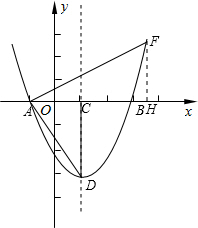
所以,这条抛物线的表达为y=x2-2x-3;
(3)过点F作作FH⊥x轴,垂足为点H,
设F(x,x2-2x-3),
∵∠FAC=∠ADC,
∴tan∠FAC=tan∠ADC,
∵tan∠ADC=
,
∴tan∠FAC=
=
,
∵FH=x2-2x-3,AH=x+1,
∴
=
,
解得x1=
,x2=-1(舍),
∴F(
,
).

∴对称轴直线l=
| -1+3 |
| 2 |
∵对称轴l与x轴相交于点C,
∴AC=2,
∵∠ACD=90°,tan∠ADC=
| 1 |
| 2 |
∴CD=4,
∵a>0,
∴D(1,-4);
(2)设y=a(x-h)2+k,有(1)可知h=1,k=-4,
∴y=a(x-1)2-4,
将x=-1,y=0代入上式,
得:a=1,

所以,这条抛物线的表达为y=x2-2x-3;
(3)过点F作作FH⊥x轴,垂足为点H,
设F(x,x2-2x-3),
∵∠FAC=∠ADC,
∴tan∠FAC=tan∠ADC,
∵tan∠ADC=
| 1 |
| 2 |
∴tan∠FAC=
| FH |
| AH |
| 1 |
| 2 |
∵FH=x2-2x-3,AH=x+1,
∴
| x2-2x-3 |
| x+1 |
| 1 |
| 2 |
解得x1=
| 7 |
| 2 |
∴F(
| 7 |
| 2 |
| 9 |
| 4 |
点评:本题考查了二次函数的综合应用,这类试题一般难度较大.解这类问题关键是善于将函数问题转化为方程问题,善于利用几何图形的有关性质、定理和二次函数的知识,并注意挖掘题目中的一些隐含条件.

练习册系列答案
相关题目