Question

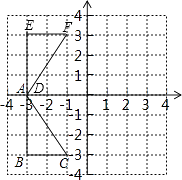
【题目】如图，在平面直角坐标系中，Rt△ABC的三个顶点坐标为 A（﹣3，0），B（﹣3，﹣3），C（﹣1，﹣3）

（1）求Rt△ABC的面积；
（2）在图中作出△ABC关于x轴对称的图形△DEF，并写出D，E，F的坐标．

Answer 1

【答案】
（1）解：S△ABC= AB×BC= ×3×2=3
（2）解：所画图形如下所示，其中△DEF即为所求，

D，E，F的坐标分别为：D（﹣3，0），E（﹣3，3），F（﹣1，3）．

【解析】（1）直接根据三角形的面积公式求解即可；（2）先找出△ABC各顶点关于x轴对称的对应点，然后顺次连接各点即可．
【考点精析】解答此题的关键在于理解三角形的面积的相关知识，掌握三角形的面积=1/2×底×高，以及对坐标与图形变化-对称的理解，了解关于x轴对称的点的特征：两个点关于x轴对称时，它们的坐标中，x相等，y的符号相反，即点P（x，y）关于x轴的对称点为P’（x，-y）；关于y轴对称的点的特征：两个点关于y轴对称时，它们的坐标中，y相等，x的符号相反，即点P（x，y）关于y轴的对称点为P’（-x，y）．