题目内容
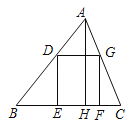
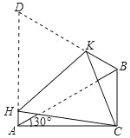
【题目】如图，在△ABC 中∠ACB＝90°、∠CAB＝30°，△ABD 是等边三角形将四边形 ACBD 折叠，使点 D 与点 C 重合，HK 为折痕，则cos∠ACH 的值是（ ）
A.
B.
C.
D.
【答案】D
【解析】
在Rt△ABC中，设BC=a，则AB=2BC=2a，AD=AB=2a．设AH=x，则HC=HD=AD-AH=2a -x．在Rt△ABC中，由勾股定理可求得得AC2=3a 2，在Rt△ACH中，由勾股定理得AH2+AC2=HC2，即x2+3a 2=（2a -x）2．解得x=
，即AH=.求得HC的值后，
求值．
∵△ABD是等边三角形，
∴∠BAD=60°，AD=AB=BD
∵∠CAB=30°，
∴∠CAH=90°.
在Rt△ABC中，∠CAB=30°，设BC=a，
∴AB=2BC=2a.
∴AD=AB=2a.
设AH=x，则HC=HD=ADAH=2ax，
在Rt△ABC中，AC2=(2a)2a2=3a2，AC=
在Rt△ACH中，AH2+AC2=HC2，即x2+3a2=(2ax) 2，
解得x=，即AH=.
∴HC=2ax=2a
，
.
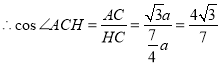故选D.
练习册系列答案
名校课堂系列答案
相关题目
