题目内容
【题目】如图,四边形ABCD是正方形,点E,F分别在BC,AB上,点M在BA的延长线上,且CE=BF=AM,过点M,E分别作NM⊥DM,NE⊥DE交于N,连接NF. 
(1)求证:DE⊥DM;
(2)猜想并写出四边形CENF是怎样的特殊四边形,并证明你的猜想.
【答案】
(1)证明:∵四边形ABCD是正方形,
∴DC=DA,∠DCE=∠DAM=90°,
在△DCE和△MDA中, 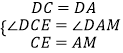 ,
,
∴△DCE≌△MDA(SAS),
∴DE=DM,∠EDC=∠MDA.
又∵∠ADE+∠EDC=∠ADC=90°,
∴∠ADE+∠MDA=90°,
∴DE⊥DM
(2)解:四边形CENF是平行四边形,理由如下:
∵四边形ABCD是正方形,
∴AB∥CD,AB=CD.
∵BF=AM,
∴MF=AF+AM=AF+BF=AB,
即MF=CD,
又∵F在AB上,点M在BA的延长线上,
∴MF∥CD,
∴四边形CFMD是平行四边形,
∴DM=CF,DM∥CF,
∵NM⊥DM,NE⊥DE,DE⊥DM,
∴四边形DENM都是矩形,
∴EN=DM,EN∥DM,
∴CF=EN,CF∥EN,
∴四边形CENF为平行四边形
【解析】(1)利用角边角可得△DCE≌△MDA,那么可得DE=DM,∠EDC=∠MDA,进而根据∠ADC=90°可得DE⊥DM;(2)先证明四边形CFMD是平行四边形,得出DM=CF,DM∥CF,再证明四边形DENM都是矩形,得出EN=DM,EN∥DM,得出CF=EN,CF∥EN,即可得出结论.
【考点精析】根据题目的已知条件,利用平行四边形的判定和正方形的性质的相关知识可以得到问题的答案,需要掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案