��Ŀ����
����Ŀ���Ķ����в��ϣ��������
����һ�����һ���������ĸ�λ���ֵ��ڳ���λ����֮���������λ����֮�ͣ���������Ϊ���������������磺��1+2=3������123��������������ͬ����55��1315Ҳ��������������
���϶�������![]() ����λ��������������������x��2��x��x+2�ֱ���������İ�λ���֣�ʮλ���֣���λ���֣����磺135��468��Ϊ����������
����λ��������������������x��2��x��x+2�ֱ���������İ�λ���֣�ʮλ���֣���λ���֣����磺135��468��Ϊ����������
���⣺
��1����֪a����������������������������������b��b��0��ʹ10a+bΪһ����������������b����Сֵ��
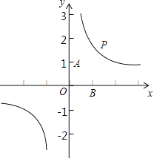
��2����֪һ����λ����������![]() ��һ�������������ĺ��ܱ�3��������c��a+d��b=4��֤��
��һ�������������ĺ��ܱ�3��������c��a+d��b=4��֤��![]() ��
��
���𰸡���1��b����СֵΪ47����2��������
�������������������1����ϸ�Ķ����ϣ����á����������͡������������ص��з�����⼴�����b����Сֵ��
��2�����ݡ����������͡������������ص㣬��ʾ��a��b��c��d��e�Ĺ�ϵ��Ȼ���������֤������.
�����������1����a�ǡ�����������
����a=![]() ��
��
��a�ǡ�����������
��x��2+x=x+2��
��x=4��
��a=246��
��10a+b=2460+b��
��2+4+6=10��9��
��10a+b�ǡ�����������
��b��40��
����2460+b�İ�λ��С��5��
��b����СֵΪ47��
��2���������������![]() ��
��
��e=a+b+c+d��
��c��a+d��b=4��
��c+d=a+b+4��
��e=2a+2b+4��
��a��b��e����λ����λ�ϵ�����
��0��a��9��0��b��9��0��e��9��������
��0��2a+2b+4��9��
��0��a+b��![]() ��
��
��a+b=1��a+b=2��
��һ����λ����������![]() ��һ�������������ĺ��ܱ�3��������һ��������������3�ı�����
��һ�������������ĺ��ܱ�3��������һ��������������3�ı�����
��a+b+c+d+e=a+b+a+b+4+2a+2b+4=4a+4b+8=4��a+b+2����3�ı�����
����a+b+2��3�ı�����
��a+b=1��
��a�����λ���֣�
��a=1��b=0��
��c+d=a+b+4=5��e=2a+2b+4=6����c�ڰ�λ��d��ʮλ��
��c=5��d=0ʱ����λ����
�������������![]() �����10506��
�����10506��
��![]() ��
��

 ȫ�ų��100��ϵ�д�
ȫ�ų��100��ϵ�д� Ӣ�ŵ��ϵ�д�
Ӣ�ŵ��ϵ�д� ������������Ծ�ϵ�д�
������������Ծ�ϵ�д�����Ŀ��2019���й������ҵ�������ң�Ϊ��ռ���г�Ӯ��������������ij��ݹ�˾��̨�����ڿ���շѱ��������������ڵĿ��ͳһ��ȡ��������8Ԫ���������������10kg�������շ��ã������������10kg����10g�IJ��ְ�0.3Ԫ/kg�շѣ�
��1��ijͬѧ��Ҫ������Ϊx��x��10��ǧ�˵��鼮����������ͬ�ǿ�ݻؼң����ͬѧ�踶��ݷ���yԪ���ú�x�Ĵ���ʽ��ʾy��
��2��������ı���Ҫ��һЩ����Ʒ������������1800ǧ�ı������ÿ�ݹ�˾�����������������������շѱ����շѱ����±�����֪����Ʒ����Ϊaǧ�ˣ������Ʒ���������������Ŀ�ݷ�Ϊ����Ԫ�����ú�a�Ĵ���ʽ��ʾw��
�۸�� | |
������ | ����� |
������10kgͳһ��ȡ5Ԫ | 0.01Ԫ/km |
����10kg������50kg�IJ���0.2Ԫ/kg | |
����50kg����0.4Ԫ/kg | |
��ע����ݷѣ�������+����ѣ� | |
����Ŀ���ҹ��ɲ��������.
(1)����ͼ��ʽ�ڷź�ɫΧ���ӣ���һ�ÿ��ͼ���輸ö����.

ͼ��˳�� |
|
|
|
|
|
��Ҫ��������/ö |
|
(2)�����㷢�ֵĹ��ɣ���һ���![]() ��ͼ������Ҫ( )ö����.
��ͼ������Ҫ( )ö����.