题目内容
如图,双曲线 经过
经过 的两个顶点
的两个顶点 、
、 轴,连接
轴,连接 ,将
,将 沿
沿 翻折后得到
翻折后得到 ,点
,点 刚好落在线段
刚好落在线段 上,连接
上,连接 ,
, 恰好平分
恰好平分 与
与 轴负半轴的夹角,若
轴负半轴的夹角,若 的面积为3,则
的面积为3,则 的值为 。
的值为 。
-6.
解析试题分析:设BC的延长线交x轴于点D,连接OC,点C(-m,n),AB=a,由角平分线的性质得,CD=CB′,则△OCD≌△OCB′,再由翻折的性质得,BC=B′C,根据反比例函数的性质,可得出S△OCD=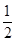 mn=
mn=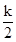 ,由AB∥x轴,得点A(a-m,2n),由题意得2n(a-m)=k,即可得出答案.
,由AB∥x轴,得点A(a-m,2n),由题意得2n(a-m)=k,即可得出答案.
试题解析:如图: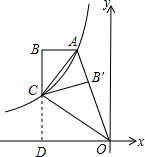
设BC的延长线交x轴于点D,
设点C(-m,n),AB=a,
∵∠ABC=90°,AB∥x轴,
∴CD⊥x轴,
由折叠的性质可得:∠AB′C=∠ABC=90°,
∴CB′⊥OA,
∵OC平分OA与x轴负半轴的夹角,
∴CD=CB′,
在Rt△OB′C和Rt△ODC中,
∵ ,
,
∴Rt△OCD≌Rt△OCB′(HL),
再由翻折的性质得,BC=B′C,
∴BC=CD,
∴点B(-m,2n)
∵双曲线 经过Rt△ABC的两个顶点A、C,
经过Rt△ABC的两个顶点A、C,
∴S△OCD=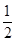 |mn|=
|mn|=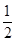 |k|
|k|
∴mn=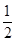 k
k
∵AB∥x轴,
∴点A(a-m,2n),
∴2n(a-m)=k
∴an=k
∴k=-6
考点: 反比例函数综合题.

练习册系列答案
相关题目
 经过点(-1,2),那么k的值等于 .
经过点(-1,2),那么k的值等于 . 为反比例函数,当k____________时,该函数图象在二、四象限内.
为反比例函数,当k____________时,该函数图象在二、四象限内. 落在反比例函数
落在反比例函数 的图像上,另“7”字形有两个顶点落在
的图像上,另“7”字形有两个顶点落在 轴上,一个顶点落在
轴上,一个顶点落在 轴上.
轴上.
 图2
图2 这样的规律拼接下去,第
这样的规律拼接下去,第 个图形中每一个小正方形的面积是 .(用含
个图形中每一个小正方形的面积是 .(用含 (k≠0)的图象上,点Q(2,4)与点P关于y轴对称,则反比例函数的表达式为________________
(k≠0)的图象上,点Q(2,4)与点P关于y轴对称,则反比例函数的表达式为________________ (x>0)的图象经过等腰梯形OABC的点A与BC的中点D.若等腰梯形OABC的面积为6,则k的值为
(x>0)的图象经过等腰梯形OABC的点A与BC的中点D.若等腰梯形OABC的面积为6,则k的值为 
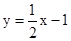 经过点C交x轴于点E,双曲线
经过点C交x轴于点E,双曲线 经过点D,则k的值为 .
经过点D,则k的值为 .
 (k>0)上,则a、b、c的大小关系为 (用“<”将a、b、c连接起来).
(k>0)上,则a、b、c的大小关系为 (用“<”将a、b、c连接起来).