��Ŀ����
����Ŀ�����ڽ�����ij�������ֲ�����ѧ���Ƴ������Żݻ����������£�
����һ������һ��ѧ������ר������ÿ�ν������ð������Żݣ�
��������������ѧ������ר������ÿ�ν������ð������Żݣ�
��ijѧ�����ڽ���![]() (��)�����շ���һ�������Ϊ
(��)�����շ���һ�������Ϊ![]() ��(Ԫ)����
��(Ԫ)����![]() �����շ������������Ϊ
�����շ������������Ϊ![]() (Ԫ) ����
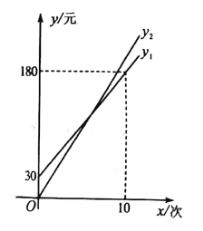
(Ԫ) ����![]() �亯��ͼ����ͼ��ʾ��
�亯��ͼ����ͼ��ʾ��
![]() ��
��![]() ��
��![]() ��ֵ����˵�����ǵ�ʵ�����壻
��ֵ����˵�����ǵ�ʵ�����壻
![]() �����ǰ��ÿ�ν������ú�
�����ǰ��ÿ�ν������ú�![]() ��ֵ��
��ֵ��
![]() ���꼶ѧ��С���ƻ�����ǰ���þ��ֲ�����
���꼶ѧ��С���ƻ�����ǰ���þ��ֲ�����![]() �Σ�Ӧѡ�����ַ���������ø���?˵�����ɣ�
�Σ�Ӧѡ�����ַ���������ø���?˵�����ɣ�
���𰸡���1��k1=15��b=30��k1=15��ʾ����ÿ�ν������ð������Ż���15Ԫ��b=30��ʾ����һ��ѧ������ר�����ķ�����30Ԫ��
��2������ǰ��ÿ�ν�������Ϊ25Ԫ��k2=20��
��3������һ������ø��٣����ɼ�������
��������
��1���ô���ϵ�������루0��30���ͣ�10��180��������㼴�����![]() ��
��![]() ��ֵ���ٸ��ݺ�����ʾ��ʵ������˵�����ɣ�
��ֵ���ٸ��ݺ�����ʾ��ʵ������˵�����ɣ�
��2�������ǰ��ÿ�ν�������ΪaԪ�����ݣ�1���������![]() Ϊ������֮��ķ��ÿ���ô���ǰ��ÿ�ν������ã�����������֮��ķ��ã����ɵõ�
Ϊ������֮��ķ��ÿ���ô���ǰ��ÿ�ν������ã�����������֮��ķ��ã����ɵõ�![]() ��ֵ��
��ֵ��
��3��д������������ϵʽ���ֱ����x=8���㣬���Ƚϴ�С������⣮
�⣺��1����ͼ��ɵã�![]() ������0��30���ͣ�10��180�����㣬���뺯����ϵʽ�ɵã�
������0��30���ͣ�10��180�����㣬���뺯����ϵʽ�ɵã�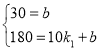 ��
��
��ã� ��
��
��k1=15��b=30��
k1=15��ʾ����ÿ�ν������ð������Ż���15Ԫ��b=30��ʾ����һ��ѧ������ר�����ķ�����30Ԫ��
��2�������ǰ��ÿ�ν�������ΪaԪ��
������ã�0.6a=15��
��ã�a=25��
������ǰ��ÿ�ν�������Ϊ25Ԫ��
k2��ʾÿ�ν����������Żݵķ��ã���k2=25��0.8=20��
��3���ɣ�1����2���ã�![]() ��
��![]() ��
��
��С������![]() �μ�x=8ʱ��
�μ�x=8ʱ��
![]() ��
��![]() ��
��
��150<160��
���һ������ø��٣�
�𣺷���һ������ø��٣�

����Ŀ��ͼ���Ǹ���ʡ����ݵ����֮������ͭ�������ֳ�����̤����������1969��10�³����������е���̨��Ĺ��1983��10�±��������ξ�ȷ��Ϊ�й����α�־���ںܶ����γ��еĹ㳡�϶�������̤���������ܣ�ijѧϰС��Ѳ��������й㳡������̤���������ܣ�ͼ�ڣ���ߵ������ĸ߶���Ϊһ�ο�����ͬѧ���ƶ��˲����������������ʵ�ز�������ý�����±���
���� | ��������̤������������ߵ������ĸ߶� | |||
����ʾ��ͼ |
| ��ͼ�����ܵ���ߵ� | ||
�������� |
|
|
| ���� |
|
| 5�� |
| |
��������ϱ��еIJ������ݣ�������С���������̤������������ߵ������ĸ߶ȣ��������һλС���������ο����ݣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��

����Ŀ�������С���С��ȥ��ˣ����ι�����������۸���������±���
����/��Ԫ/ǧ�ˣ� | 4 | 3 | 2 | �ϼ� |
С�칺�������/ǧ�� | 1 | 2 | 3 | 6 |
С�ݹ��������/ǧ�� | 2 | 2 | 2 | 6 |
��1��С���С�ݹ�����������������λ���������Ƕ��٣�
��2����ƽ���۸�˭���������Ҫ����Щ.��˼������С����С����˵��������Ϊ˭˵�öԣ�Ϊʲô��
С����˵��
ÿ�ι�����ͬ����������Ҳ��ͬ��ƽ���۸�Ӧ��Ҳһ��������![]() ��Ԫ/ǧ�ˣ����������˹����������һ������.
��Ԫ/ǧ�ˣ����������˹����������һ������.
С����˵��
�����������Ȼ��ͬ����С�컨��16Ԫ��С�ݻ���18Ԫ��ƽ���۸�һ��������С�칺�������������.
��3��С����ֱ������ϵ�л���������������ͼ��ͼ����![]() ����ͼ������
����ͼ������![]() �ĺᡢ������ֱ�ΪС���С�ݹ����������۸��ƽ����.
�ĺᡢ������ֱ�ΪС���С�ݹ����������۸��ƽ����.
����˷����������Ĺ�ϵʽ��
���жϵ�![]() �Ƿ��ڴ˺���ͼ����.
�Ƿ��ڴ˺���ͼ����.
����Ŀ����2017��1��1�����ҹ���ʻ֤������ʽʵʩ�µļݿ���ѵģʽ���¹涨C2��ʻ֤����ѵѧʱΪ40ѧʱ����У��ѧ�ѱ��ֲ�ͬʱ�Σ���ͨʱ��aԪ/ѧʱ���߷�ʱ�κͽڼ���ʱ�ζ�ΪbԪ/ѧʱ��
��1��С����С�����ڴ˼�У�μ�C2��ʻ֤����ѵ���±���С����С������ѵ���������ѵѧʱ��Ϊ40������������ṩ����Ϣ�������a��b��ֵ��
ѧԱ | ��ѵʱ�� | ��ѵѧʱ | ��ѵ�ܷ��� |
С�� | ��ͨʱ�� | 20 | 6000Ԫ |
�߷�ʱ�� | 5 | ||
�ڼ���ʱ�� | 15 | ||
С�� | ��ͨʱ�� | 30 | 5400Ԫ |
�߷�ʱ�� | 2 | ||
�ڼ���ʱ�� | 8 |
��2��С�±����μ���C2��ʻ֤����ѵ�����Ҽƻ�ѧ��ȫ������ѧʱ����Ϊ�˲�����������ͨʱ�ε���ѵѧʱ���ᳬ����������ʱ����ѧʱ��![]() ����С����ͨʱ����ѵ��xѧʱ����ѵ�ܷ���ΪyԪ
����С����ͨʱ����ѵ��xѧʱ����ѵ�ܷ���ΪyԪ
����y��x֮��ĺ�����ϵʽ����ȷ���Ա���x��ȡֵ��Χ��
��С�����ѡ����ѵʱ�Σ�����ʹ�ñ�����ѵ���ܷ�����ͣ�



