Question

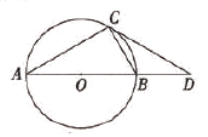
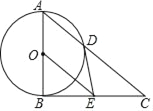
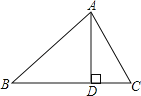
【题目】如图，在△ABC中，AD⊥BC于D，下列条件：（1）∠B+∠DAC＝90°；（2）∠B＝∠DAC；（3）；（4）AB2＝BDBC．其中一定能够判定△ABC是直角三角形的有（填序号）_____．

Answer 1

【答案】（2）（3）（4）

【解析】

（1）根据直角三角形中两个锐角互余，即可判定∠BAD＝∠CAD，继而可得△ABC是等腰三角形，不能判定△ABC是直角三角形；

（2）利用直角三角形中两个锐角互余的知识，可得∠BAC＝90°，则可得△ABC是直角三角形；

（3）由，可得，推出sin∠ACD＝sin∠B，即∠ACD＝∠B，由此即可判定．

（4）由AB2＝BDBC与∠B是公共角，可判定△CBA∽△ABD，△ABD是直角三角形，则可得△ABC是直角三角形．

解：（1）不能，

∵AD⊥BC，

∴∠B+∠BAD＝90°，

∵∠B+∠DAC＝90°，

∴∠BAD＝∠DAC，

∴△ABD≌△ACD（ASA），

∴AB＝AC，

∴△ABC是等腰三角形，

∴无法证明△ABC是直角三角形；

（2）能，

∵AD⊥BC，

∴∠B+∠BAD＝90°，

∵∠B＝∠DAC，

∴∠BAC＝∠BAD+∠DAC＝∠BAD+∠B＝90°；

（3）能，

∵，

∴，

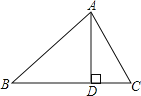
∵AD⊥BC，∴∠ADB＝∠ADC＝90°，

在Rt△ACD中

sin∠CAD＝，

在Rt△ABD中，sin∠B＝，

∴sin∠ACD＝sin∠B，

∴∠ACD＝∠B，

∵∠B+∠BAD＝90°，

∴∠CAD+∠BAD＝90°，

∴∠BAC＝90°，

∴△ABC是直角三角形．

（4）能，

∵能说明△CBA∽△ABD，

又∵△ABD是直角三角形，

∴△ABC一定是直角三角形．

∴一定能够判定△ABC是直角三角形的有（2）（4）（3）．

故答案为：（2）（3）（4）．