题目内容
 在等腰△ABC中,AB=AC,BE、CD分别是底角的平分线,DE∥BC,图中等腰三角形有
在等腰△ABC中,AB=AC,BE、CD分别是底角的平分线,DE∥BC,图中等腰三角形有
- A.3个
- B.4个
- C.5个
- D.6个
D
分析:图中的等腰三角形有6个,分别为:△ABC,△ADE,△BDE,△DEC,△DEF,△BFC,理由为:由AB=AC,利用等边对等角得到一对角相等,再由DE与BC平行,利用两直线平行同位角相等得到两对角相等,等量代换及等角对等边得到AD=AE,即△ADE为等腰三角形,由BE与CD分别为角平分线,利用角平分线定义得到两对角相等,再由两直线平行内错角相等,利用等量代换及等角对等边得到BD=ED,DE=CE,以及DF=EF,BF=CF,可得出△BDE,△DEC,△DEF,△BFC都为等腰三角形.
解答: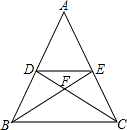 解:图中的等腰三角形有6个,分别为:△ABC,△ADE,△BDE,△DEC,△DEF,△BFC,理由为:
解:图中的等腰三角形有6个,分别为:△ABC,△ADE,△BDE,△DEC,△DEF,△BFC,理由为:
∵AB=AC,
∴∠ABC=∠ACB,
又DE∥BC,
∴∠ADE=∠ABC,∠AED=∠ACB,
∴∠ADE=∠AED,即△ADE为等腰三角形;
又BE、CD分别是底角的平分线,
∴∠DBE=∠EBC= ∠ABC,∠ACD=∠DCB=
∠ABC,∠ACD=∠DCB= ∠ACB,
∠ACB,
∴∠EBC=∠DCB=∠DBE=∠ACD,
∴BF=CF,即△BFC为等腰三角形;
又DE∥BC,
∴∠EDC=∠DCB,∠DEB=∠EBC,
∴∠DEB=∠EDC=∠DCB=∠EBC,
∴DF=EF,BD=ED,DE=CE,
则△DEF、△BDE、△DEC都为等腰三角形.
故选D
点评:此题考查了等腰三角形的判定与性质,平行线的性质,以及角平分线定义,利用了等量代换的思想,熟练掌握等腰三角形的判定与性质是解本题的关键.
分析:图中的等腰三角形有6个,分别为:△ABC,△ADE,△BDE,△DEC,△DEF,△BFC,理由为:由AB=AC,利用等边对等角得到一对角相等,再由DE与BC平行,利用两直线平行同位角相等得到两对角相等,等量代换及等角对等边得到AD=AE,即△ADE为等腰三角形,由BE与CD分别为角平分线,利用角平分线定义得到两对角相等,再由两直线平行内错角相等,利用等量代换及等角对等边得到BD=ED,DE=CE,以及DF=EF,BF=CF,可得出△BDE,△DEC,△DEF,△BFC都为等腰三角形.
解答:
 解:图中的等腰三角形有6个,分别为:△ABC,△ADE,△BDE,△DEC,△DEF,△BFC,理由为:
解:图中的等腰三角形有6个,分别为:△ABC,△ADE,△BDE,△DEC,△DEF,△BFC,理由为:∵AB=AC,
∴∠ABC=∠ACB,
又DE∥BC,
∴∠ADE=∠ABC,∠AED=∠ACB,
∴∠ADE=∠AED,即△ADE为等腰三角形;
又BE、CD分别是底角的平分线,
∴∠DBE=∠EBC=
 ∠ABC,∠ACD=∠DCB=
∠ABC,∠ACD=∠DCB= ∠ACB,
∠ACB,∴∠EBC=∠DCB=∠DBE=∠ACD,
∴BF=CF,即△BFC为等腰三角形;
又DE∥BC,
∴∠EDC=∠DCB,∠DEB=∠EBC,
∴∠DEB=∠EDC=∠DCB=∠EBC,
∴DF=EF,BD=ED,DE=CE,
则△DEF、△BDE、△DEC都为等腰三角形.
故选D
点评:此题考查了等腰三角形的判定与性质,平行线的性质,以及角平分线定义,利用了等量代换的思想,熟练掌握等腰三角形的判定与性质是解本题的关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
 8、如图所示,在等腰△ABC中,点D是BC的中点,DE⊥AB,DF⊥AC,垂足分别为E、F,图中有几对全等三角形( )
8、如图所示,在等腰△ABC中,点D是BC的中点,DE⊥AB,DF⊥AC,垂足分别为E、F,图中有几对全等三角形( ) (2013•闸北区二模)如图,在等腰△ABC中,底边BC的中点是点D,底角的正切值是
(2013•闸北区二模)如图,在等腰△ABC中,底边BC的中点是点D,底角的正切值是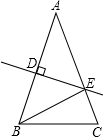 如图,在等腰△ABC中,AB=AC=10cm,直线DE垂直平分AB,分别交AB、AC于D、E两点.若BC=8cm,则△BCE的周长是
如图,在等腰△ABC中,AB=AC=10cm,直线DE垂直平分AB,分别交AB、AC于D、E两点.若BC=8cm,则△BCE的周长是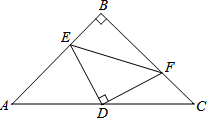 如图,在等腰△ABC中,∠ABC=90°,D为底边AC中点,过D点作DE⊥DF,交AB于E,交BC于F.若AE=12,FC=5,
如图,在等腰△ABC中,∠ABC=90°,D为底边AC中点,过D点作DE⊥DF,交AB于E,交BC于F.若AE=12,FC=5,