题目内容
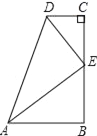
【题目】如图,AH是⊙O的直径,矩形ABCD交⊙O于点E,连接AE,将矩形ABCD沿AE折叠,点B落在CD边上的点F处,画直线EF. 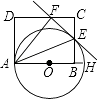
(1)求证:直线EF是⊙O的切线.
(2)若CD=10,EB=5,求⊙O的直径.
【答案】
(1)证明:
如图,连接OE,
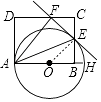
∵OA=OE,
∴∠EAO=∠AEO,
由折叠可得∠EAO=∠FAE,
∴∠FAE=∠AEO,
∴AF∥OE,
∴∠AFE+∠OEF=180°,
在矩形ABCD中,∠ABC=90°,
由折叠可知∠AFE=∠ABC=90°,
∴∠OEF=90°,
∴OE⊥EF,且点E在圆上,OE为半径,
∴EF是⊙O的切线
(2)解:∵四边形ABCD是矩形,CD=10,
∴AB=CD=10,∠ABE=90°,
设OA=OE=x,则OB=10﹣x,
在Rt△OBE中,∠OBE=90°,EB=5,
由勾股定理可得OB2+BE2=OE2,
∴(10﹣x)2+52=x2,解得x= ![]() ,
,
∴AH=2x= ![]() ,
,
∴⊙O的直径为 ![]()
【解析】(1)连接OE,由折叠的性质结合条件可证得OE∥AF,再由条件可得AF⊥EF,则可证得结论;(2)可设OA=OE=x,则OB=10﹣x,在Rt△OBE中,可求得x的值,进一步可求得⊙O的直径.
【考点精析】本题主要考查了矩形的性质和翻折变换(折叠问题)的相关知识点,需要掌握矩形的四个角都是直角,矩形的对角线相等;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.

【题目】某商店分两次购进![]() 、
、![]() 两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
购进数量(件) | 购进所需费用(元) | ||
|
| ||
第一次 | 30 | 40 | 3800 |
第二次 | 40 | 30 | 3200 |
(1)求![]() 、
、![]() 两种商品每件的进价分别是多少元?
两种商品每件的进价分别是多少元?
(2)商场决定![]() 种商品以每件30元出售,
种商品以每件30元出售,![]() 种商品以每件100元出售.为满足市场需求,需购进
种商品以每件100元出售.为满足市场需求,需购进![]() 、
、![]() 两种商品共1000件,且
两种商品共1000件,且![]() 种商品的数量不少于
种商品的数量不少于![]() 种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按![]() 元/公里计算,耗时费按
元/公里计算,耗时费按![]() 元/分钟计算(总费用不足
元/分钟计算(总费用不足![]() 元按
元按![]() 元计价).小敏、小刚两人用该打车方式出行,按上述计价规则,其行驶里程数、耗时以及打车总费用如下表:
元计价).小敏、小刚两人用该打车方式出行,按上述计价规则,其行驶里程数、耗时以及打车总费用如下表:
里程数 | 耗时 | 车费(元) | |
小敏 |
|
|
|
小刚 |
|
|
|
![]() 求
求![]() 的值;
的值;
![]() 若小华也用该打车方式打车,平均车速为
若小华也用该打车方式打车,平均车速为![]() 公里/时,行驶了
公里/时,行驶了![]()