题目内容
【题目】对于二次函数y=x2-3x+2和一次函数y=-2x+4,把y=t(x2-3x+2)+(1-t)(-2x+4)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线E.
现有点A(2,0)和抛物线E上的点B(-1,n),请完成下列任务:
(1)【尝试】
①当t=2时,抛物线E的顶点坐标是.
②点A抛物线E上;(填“在”或“不在”),
③n=.
(2)【发现】通过②和③的演算可知,对于t取任何不为零的实数,抛物线E总过定点,这个定点的坐标是.
(3)【应用1】二次函数y=-3x2+5x+2是二次函数y=x2-3x+2和一次函数y=-2x+4的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由.
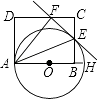
(4)【应用2】以AB为一边作矩形ABCD,使得其中一个顶点落在y轴上,若抛物线E经过点A、B、C,求出所有符合条件的t的值.
【答案】
(1)(1,-2),在,6
(2)(2,0)、(-1,6)
(3)解:将x=2代入y=-3x2+5x+2,y=0,即点A在抛物线上.
将x=-1代入y=-3x2+5x+2,计算得:y=-6≠6,
即可得抛物线y=-3x2+5x+2不经过点B,
二次函数y=-3x2+5x+2不是二次函数y=x2-3x+2和一次函数y=-2x+4的一个“再生二次函数”
(4)解:如图,作矩形ABC1D1和ABC2D2,过点B作BK⊥y轴于点K,过B作BM⊥x轴于点M,
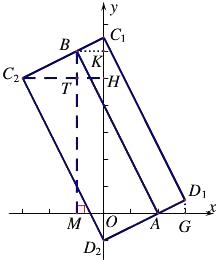
易得AM=3,BM=6,BK=1,△KBC1∽△MBA,
则: ![]()
即 ![]()
求得 C 1,K= ![]()
所以点C1(0, ![]() ).
).
易知△KBC1≌△GAD1,得AG=1,GD1= ![]() ,
,
∴点D1(3, ![]() ).
).
易知△OAD2∽△GAD1, ![]() ,
,
由AG=1,OA=2,GD1= ![]() ,
,
求得 OD2=1,
∴点D2(0,-1).
易知△TBC2≌△OD2A,得TC2=AO=2,BT=OD2=1,
所以点C2(-3,5).
∵抛物线E总过定点A(2,0)、B(-1,6),
∴符合条件的三点可能是A、B、C或A、B、D
当抛物线E经过A、B、C1时,将C1(0, ![]() )代入y=t(x2-3x+2)+(1-t)(-2x+4),求得t1=-
)代入y=t(x2-3x+2)+(1-t)(-2x+4),求得t1=- ![]() ;
;
当抛物线E经过A、B、D1,A、B、C2,A、B、D2时,可分别求得t2= ![]() ,t3=-
,t3=- ![]() ,t4=
,t4= ![]() .
.
∴满足条件的所有t的值为:- ![]() ;
; ![]() ,-
,- ![]() ,
, ![]()
【解析】解:(1)【尝试】①将t=2代入抛物线E中,得:y=t(x2-3x+2)+(1-t)(-2x+4)=2x2-4x=2(x-1)2-2,
∴此时抛物线的顶点坐标为:(1,-2).
②将x=2代入y=t(x2-3x+2)+(1-t)(-2x+4),得 y=0,
∴点A(2,0)在抛物线E上.
③将x=-1代入抛物线E的解析式中,得:
n=t(x2-3x+2)+(1-t)(-2x+4)=6.(2)【发现】将抛物线E的解析式展开,得:
y=t(x2-3x+2)+(1-t)(-2x+4)=t(x-2)(x+1)-2x+4
∴抛物线E必过定点(2,0)、(-1,6).

 阅读快车系列答案
阅读快车系列答案【题目】某校为了解九年级学生的身体素质情况,体育老师对九(1)班50位学生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成如图所示的频数分布表和扇形统计图.
等第 | 成绩(得分) | 频数(人数) | 频率 |
A | 10分 | 7 | 0.14 |
9分 | x | m | |
B | 8分 | 15 | 0.30 |
7分 | 8 | 0.16 | |
C | 6分 | 4 | 0.08 |
5分 | y | n | |
5分以下 | 3 | 0.06 | |
合计 | 50 | 1 |
(1)直接写出:m,x,y;
(2)求表示得分为C等的扇形的圆心角的度数;
(3)如果该校九年级共有700名学生,试估计这700名学生中成绩达到A等和B等的人数共有多少人?
![]()
【题目】一次期中考试中,甲、乙、丙、丁、戊五位同学的数学、英语成绩等有关信息如下表所示(单位:分):
(1)求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式:标准分=(个人成绩-平均成绩)÷成绩标准差.
从标准分看,标准分大的考试成绩更好,请问甲同学在本次考试中,数学与英语哪个学科考得更好?
甲 | 乙 | 丙 | 丁 | 戊 | 平均分 | 标准差 | |
数学 | 71 | 72 | 69 | 68 | 70 | ||
英语 | 88 | 82 | 94 | 85 | 76 | 85 |