题目内容
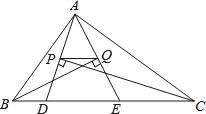
【题目】如图,△ABC的周长为32,点D,E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=12,则PQ的长为( )
A. 2B. 3C. 4D. 5
【答案】C
【解析】
首先判断△BAE、△CAD是等腰三角形,从而得出BA=BE,CA=CD,由△ABC的周长为32,及BC=12,可得DE=8,利用中位线定理可求出PQ.
∵BQ平分∠ABC,BQ⊥AE,
∴∠ABQ=∠EBQ,
∵∠ABQ+∠BAQ=90°,∠EBQ+∠BEQ=90°,
∴∠BAQ=∠BEQ,
∴AB=BE,同理:CA=CD,
∴点Q是AE中点,点P是AD中点(三线合一),
∴PQ是△ADE的中位线,
∵BE+CD=AB+AC=3212=20,
∴DE=BE+CDBC=8,
∴PQ=![]() DE=4.
DE=4.
故选:C.

练习册系列答案
相关题目