题目内容
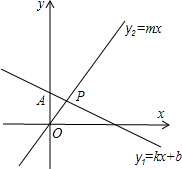 如图,直线y1=kx+b过点A(0,2),且与直线y2=mx交于点P(1,m),则不等式组mx>kx+b>mx-2的解集是
如图,直线y1=kx+b过点A(0,2),且与直线y2=mx交于点P(1,m),则不等式组mx>kx+b>mx-2的解集是分析:由于一次函数y1同时经过A、P两点,可将它们的坐标分别代入y1的解析式中,即可求得k、b与m的关系,将其代入所求不等式组中,即可求得不等式的解集.
解答:解:由于直线y1=kx+b过点A(0,2),P(1,m),
则有:
,
解得
.
∴直线y1=(m-2)x+2.
故所求不等式组可化为:mx>(m-2)x+2>mx-2,
解得:1<x<2.
则有:
|
解得
|
∴直线y1=(m-2)x+2.
故所求不等式组可化为:mx>(m-2)x+2>mx-2,
解得:1<x<2.
点评:解决此题的关键是确定k、b与m的关系,从而通过解不等式组得到其解集.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 如图,直线y1=kx+b过点A(0,2),且与直线y2=mx交于点P(1,m),则不等式组mx>kx+b>mx-2的解集是( )
如图,直线y1=kx+b过点A(0,2),且与直线y2=mx交于点P(1,m),则不等式组mx>kx+b>mx-2的解集是( )| A、1<X<2 | B、0<X<2 | C、0<X<1 | D、1<X |
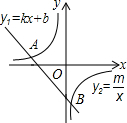 如图,直线y1=kx+b与双曲线y2=
如图,直线y1=kx+b与双曲线y2=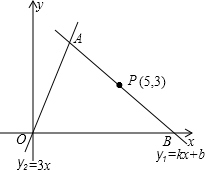 点B.设点A的横坐标为m(m>1且m≠5).
点B.设点A的横坐标为m(m>1且m≠5). 12、如图,直线y1=kx+b与y2=-x-1交于点P,它们分别与x轴交于A、B,且B、P、A三点的横坐标分别为-1,-2,-3,则满足y1>y2的x的取值范围是
12、如图,直线y1=kx+b与y2=-x-1交于点P,它们分别与x轴交于A、B,且B、P、A三点的横坐标分别为-1,-2,-3,则满足y1>y2的x的取值范围是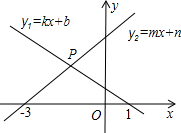 如图,直线y1=kx+b与y2=mx+n相交于点P,则不等式组
如图,直线y1=kx+b与y2=mx+n相交于点P,则不等式组