题目内容
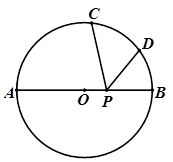
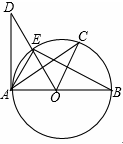
如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径是2 cm,则弦CD的长为
cm,则弦CD的长为

 cm,则弦CD的长为
cm,则弦CD的长为
A.2 cm cm | B.6cm | C.3cm | D. cm cm |
B
试题分析:由∠CDB=30°可得∠COB=60°,再根据∠COB的正弦函数即可求得CE的长,最后根据垂径定理即可求的结果.
∵∠CDB=30°
∴∠COB=60°
∵
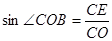 ,
,
∴
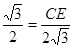 ,解得
,解得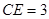
∵AB是⊙O的直径,弦CD⊥AB于点E
∴
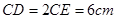
故选B.
点评:解题的关键是熟记同弧或等弧所对是圆周角等于所对圆心角的一半,垂直于弦的直径平分弦.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
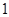 ,母线长为
,母线长为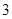 ,则这个圆锥的侧面积是 .(结果保留
,则这个圆锥的侧面积是 .(结果保留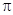 )
)
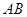 是⊙O的直径,弦BC=8,∠BOC=60°, OE⊥AC,垂足为E.
是⊙O的直径,弦BC=8,∠BOC=60°, OE⊥AC,垂足为E.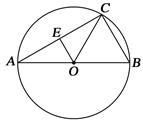
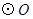 上,若∠ACB=46°,则∠AOB的度数是
上,若∠ACB=46°,则∠AOB的度数是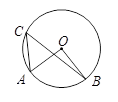
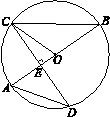
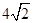 ,AE=2,求⊙O的半径.
,AE=2,求⊙O的半径. 的半径为4,
的半径为4,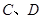 是直径
是直径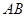 同侧圆周上的两点,弧
同侧圆周上的两点,弧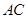 的度数为
的度数为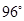 ,弧
,弧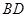 的度数为
的度数为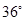 ,动点
,动点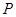 在
在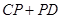 的最小值为 。
的最小值为 。