题目内容
【题目】已知矩形
中，
是
边上的一个动点，点
、
、
分别是
、
、
的中点．
（1）求证：
．
（2）若
，当四边形
是正方形时，求矩形的面积．
【答案】（1）见解析；（2）8．
【解析】
（1）根据三角形中位线定理和全等三角形的判定证明即可；
（2）利用正方形的性质和矩形的面积公式解答即可．
解：（1）连接EF，
∵点F，G，H分别是BC，BE，CE的中点，
∴FH∥BE，FH=
BE，FH=BG，
∴∠CFH=∠CBG，
∵BF=CF，
∴△BGF≌△FHC（SAS），
（2）当四边形EGFH是正方形时，连接GH，可得：EF⊥GH且EF=GH，
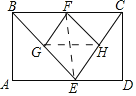
∵在△BEC中，点，H分别是BE，CE的中点，
∴GH=BC＝AD＝2，且GH∥BC，
∴EF⊥BC，
∵AD∥BC，AB⊥BC，
∴AB=EF=GH=2，
∴矩形ABCD的面积=ABAD＝2×4＝8．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
