题目内容
【题目】某市水产养殖户进行小龙虾养殖.已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价p(元/千克)与时间第t(天)之间的函数关系为: ,日销售量y(千克)与时间第t(天)之间的函数关系如图所示:
,日销售量y(千克)与时间第t(天)之间的函数关系如图所示:
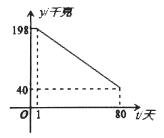
(1)求日销售量y与时间t的函数关系式?
(2)哪一天的日销售利润最大?最大利润是多少?
(3)该养殖户有多少天日销售利润不低于2400元?
【答案】(1)y=﹣2t+200(1≤x≤80,t为整数);(2)第30天的日销售利润最大,最大利润为2450元.(3)共有21天符合条件.
【解析】
(1)根据函数图象,利用待定系数法求解可得;
(2)设日销售利润为w,分1≤t≤40和41≤t≤80两种情况,根据“总利润=每千克利润×销售量”列出函数解析式,由二次函数的性质分别求得最值即可判断;
(3)求出w=2400时t的值,结合函数图象即可得出答案.
(1)设解析式为y=kt+b,将(1,198)、(80,40)代入,得:
![]() ,
,
解得:![]() ,
,
∴y=﹣2t+200(1≤x≤80,t为整数);
(2)设日销售利润为w,则w=(p﹣6)y,
①当1≤t≤40时,w=(![]() t+16﹣6)(﹣2t+200)=﹣
t+16﹣6)(﹣2t+200)=﹣![]() (t﹣30)2+2450,
(t﹣30)2+2450,
∴当t=30时,w最大=2450;
②当41≤t≤80时,w=(﹣![]() t+46﹣6)(﹣2t+200)=(t﹣90)2﹣100,
t+46﹣6)(﹣2t+200)=(t﹣90)2﹣100,
∴当t=41时,w最大=2301,
∵2450>2301,
∴第30天的日销售利润最大,最大利润为2450元.
(3)由(2)得:当1≤t≤40时,w=﹣![]() (t﹣30)2+2450,
(t﹣30)2+2450,
令w=2400,即﹣![]() (t﹣30)2+2450=2400,解得:t1=20、t2=40,
(t﹣30)2+2450=2400,解得:t1=20、t2=40,
由函数w=﹣![]() (t﹣30)2+2450图象可知,当20≤t≤40时,日销售利润不低于2400元,
(t﹣30)2+2450图象可知,当20≤t≤40时,日销售利润不低于2400元,
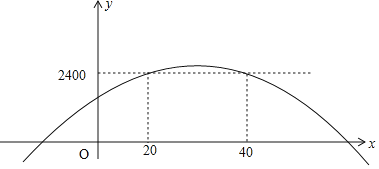
而当41≤t≤80时,w最大=2301<2400,
∴t的取值范围是20≤t≤40,
∴共有21天符合条件.

 阅读快车系列答案
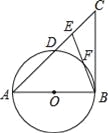
阅读快车系列答案【题目】如图,在△ABC中,E是AC边上的一点,且AE=AB,∠BAC=2∠CBE,以AB为直径作⊙O交AC于点D,交BE于点F.
(1)求证:BC是⊙O的切线;
(2)若AB=8,BC=6,求DE的长.
【题目】某景点的门票价格如表
购票人数/人 | 1~40 | 41~80 | 80以上 |
每人门票价/元 | 10 | 8 | 6 |
某校九年级(1)、(2)两班计划去春游该景点,其中(1)班人数少于40人,(2)班人数多于40人且少于80人,如果两班都以班为单位单独购票,则一共支付838元:如果两班联合起来作为一个团体购票,则只需花费570元
(1)两个班各有多少名学生;
(2)团体购票与单独购票相比较,两个班各节约了多少钱?