题目内容
【题目】(阅读材料)
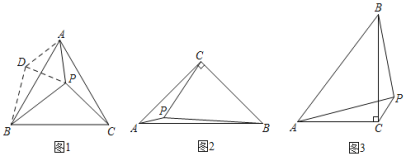
小明遇到这样一个问题:如图1,点P在等边三角形ABC内,且∠APC=150°,PA=3,PC=4,求PB的长.
小明发现,以AP为边作等边三角形APD,连接BD,得到△ABD;由等边三角形的性质,可证△ACP≌△ABD,得PC=BD;由已知∠APC=150°,可知∠PDB的大小,进而可求得PB的长.
(1)请回答:在图1中,∠PDB= °,PB= .
(问题解决)
(2)参考小明思考问题的方法,解决下面问题:
如图2,△ABC中,∠ACB=90°,AC=BC,点P在△ABC内,且PA=1,PB=![]() ,PC=
,PC=![]() ,求AB的长.
,求AB的长.
(灵活运用)
(3)如图3,在Rt△ABC中,∠ACB=90°,∠BAC=α,且tanα=![]() ,点P在△ABC外,且PB=3,PC=1,直接写出PA长的最大值.
,点P在△ABC外,且PB=3,PC=1,直接写出PA长的最大值.
【答案】(1)90°,5;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由△ACP≌△ABD,得∠ADB=∠APC=150°,PC=BD=4,AD=AP=3,因为△ADP为等边三角形,所以∠ADP=60°,DP=AD=3,可得∠BDP=90°,在Rt△BDP中,用勾股定理可求得PB的长;
(2)如图2中,把△ACP绕点C逆时针旋转90°得到△BCD.首先证明∠PDB=90°,再证明A,P,D共线,利用勾股定理即可解决问题.
(3)如图3中,作CD⊥CP,使得CD=![]() PC=
PC=![]() ,则PD=
,则PD=![]() ,利用相似三角形的性质求出AD,即可解决问题.
,利用相似三角形的性质求出AD,即可解决问题.
(1)如图1中,
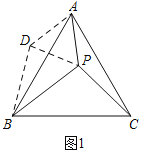
∵△ACP≌△ABD,
∴∠PDB=∠APC=150°,PC=BD=4,AD=AP=3,
∵△ADP为等边三角形,
∴∠ADP=60°,DP=AD=3,
∴∠BDP=150°﹣60°=90°,
∴PB=![]() =5.
=5.
(2)如图2中,把△ACP绕点C逆时针旋转90°得到△BCD.
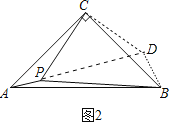
由旋转性质可知;BD=PA=1,CD=CP=2![]() ,∠PCD=90°,
,∠PCD=90°,
∴△PCD是等腰直角三角形,
∴PD=![]() PC=
PC=![]() ×2
×2![]() =4,∠CDP=45°,
=4,∠CDP=45°,
∵PD2+BD2=42+12=17,PB2=(![]() )2=17,
)2=17,
∴PD2+BD2=PB2,
∴∠PDB=90°,
∴∠BDC=135°,
∴∠APC=∠CDB=135°,∵∠CPD=45°,
∴∠APC+∠CPD=180°,
∴A,P,D共线,
∴AD=AP+PD=5,
在RtADB中,AB=![]() .
.
(3)如图3中,作CD⊥CP,使得CD=![]() PC=
PC=![]() ,则PD=
,则PD=![]() ,
,
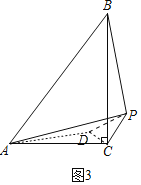
∵tan∠BAC=![]() ,
,
∴![]() ,
,
∵∠ACB=∠PCD=90°,
∴∠ACD=∠BCP,
∴△ACD∽△BCP,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴PA的最大值为![]() .
.