题目内容
【题目】如图,在△ABC中,AD平分∠BAC,过B作BE⊥AD于E,过E作EF∥AC交AB于F,则下列结论:(1)AF=FE,(2)FE=FB,(3)FE=BE,(4)AF=BF,(5)BE =BF,成立的有( )

A.1 个B.2 个C.3个D.4个
【答案】C
【解析】
根据角平分线的定义可得∠1=∠2,根据两直线平行,内错角相等可得∠2=∠3,从而得到∠1=∠3,再根据等角对等边可得AF=FE,根据垂直定义和直角三角形两锐角互余可得∠3+∠5=90°,∠1+∠4=90°,从而求出∠4=∠5,再根据等角对等边可得FB=FE,对各结论逐一判断即可.
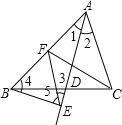
解:如图,∵AD平分∠BAC,
∴∠1=∠2,
∵EF∥AC,
∴∠2=∠3,
∴∠1=∠3,
∴AF=FE,故(1)正确;
∵BE⊥AD,
∴∠3+∠5=90°,∠1+∠4=90°,
∴∠4=∠5,
∴FE=FB,故(2)正确;
∴AF=BF=FE,故(4)正确,
∵无法判断出△BEF是等边三角形,
∴FE=BE与BE=BF不一定成立,故(3)(5)错误;
综上所述,正确的是(1)(2)(4)共3个.
故选:C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目