Question

【题目】如图，菱形对角线、的交点是四边形对角线的中点，四个顶点、、、分别在四边形的边、、、上．

求证：四边形是平行四边形；

如图若四边形是矩形，当与重合时，已知，且菱形的面积是，求矩形的长与宽．

Answer 1

【答案】（1）见解析；（2）长为，宽为4

【解析】

（1）根据菱形的性质可得出OA＝OC，OD＝OB，再由中点的性质可得出OF＝OH，结合对顶角相等即可利用全等三角形的判定定理（SAS）证出△AOF≌△COH，从而得出AF∥CH，同理可得出DH∥BF，依据平行四边形的判定定理即可证出结论；

（2）设BD＝m（m＞0），则AC＝2m，结合菱形的面积为20即可求出m＝2，进而得出AC、BD的长度，再由勾股定理即可得出AB的长度，由四边形EFGH为矩形即可得出△AOB∽△AGC，根据相似比即可得出＝，代入数据，此题得解.

∵点是菱形对角线、的交点，

∴，，

∵点是线段的中点，

∴．

在和中，有，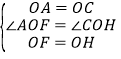

∴，

∴，

∴．

同理可得：．

∴四边形是平行四边形．

设BD＝m，则AC＝2m，

∴S菱形ABCD＝ACBD＝m2＝20，

∴m＝2，

即BD＝2，AC＝4．

∵四边形ABCD为菱形，

∴OB＝BD＝，OA＝AC＝2，

∴AB＝＝5．

∵四边形EFGH为矩形，

∴∠G＝∠AOB＝90°，

∴△AOB∽△AGC，

∴＝，

∴CG＝4，AG＝8．

∴矩形EFGH的长为8，宽为4.