题目内容
【题目】如图,某数学活动小组要测量楼AB的高度,楼AB在太阳光的照射下在水平面的影长BC为6米,在斜坡CE的影长CD为13米,身高1.5米的小红在水平面上的影长为1.35米,斜坡CE的坡度为1:2.4,求楼AB的高度.(坡度为铅直高度与水平宽度的比)
【答案】解:作DN⊥AB,垂足为N,作CM⊥DN,垂足为M,
则CM:MD=1:2.4=5:12,
设CM=5x,则MD=12x,
由勾股定理得CD= ![]() =13x=13
=13x=13
∴x=1
∴CM=5,MD=12,
四边形BCMN为矩形,MN=BC=6,BN=CM=5,
太阳光线为平行光线,光线与水平面所成的角度相同,
角度的正切值相同,∴AN:DN=1.5:1.35=10:9,
∴9AN=10DN=10×(6+12)=180,
AN=20,AB=20﹣5=15,
答:楼AB的高度为15米.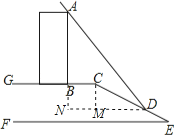
【解析】作DN⊥AB,垂足为N,作CM⊥DN,垂足为M,设CM=5x,根据坡度的概念求出CM、DM,根据平行线的性质列出比例式,计算即可.
【考点精析】利用关于坡度坡角问题对题目进行判断即可得到答案,需要熟知坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面与水平面的夹角记作A(叫做坡角),那么i=h/l=tanA.

练习册系列答案
相关题目




