Question

【题目】已知点A（2，a）在抛物线y=x2上
（1）求A点的坐标；
（2）在x轴上是否存在点P，使△OAP是等腰三角形？若存在写出P点坐标；若不存在，说明理由．

Answer 1

【答案】
（1）

解：∵点A（2，a）在抛物线y=x2上，

∴a=22=4，

∴A点的坐标为：（2，4）；

（2）

解：如图所示：

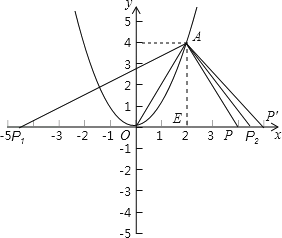
以O为顶点时，

AO=P1O= 或AO=AP2=

∴点P坐标：（ ，0），（﹣ ，0），

以A为顶点时，AO=OP，

∴点P坐标：（4，0）；

以P为顶点时，OP′=AP′，

∴AE2+P′E2=P′A2，设AP′=x，

则42+（x﹣2）2=x2，

解得：x=5，

∴点P坐标：（5，0），

综上所述：使△OAP是等腰三角形则P点坐标为：（ ，0），（﹣ ，0），（4，0），（5，0）．

【解析】（1）直接将A点代入解析式求出即可A点坐标即可；（2）分别根据以O为顶点时，以A为顶点时，以P为顶点时求出符合题意的点的坐标即可．