Question

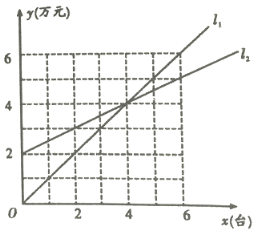
【题目】如图，在平面直角坐标系中，点的坐标为，以点为圆心，8为半径的圆与轴交于，两点，过作直线与轴负方向相交成的角，且交轴于点，以点为圆心的圆与轴相切于点.

（1）求直线的解析式；

（2）将以每秒1个单位的速度沿轴向左平移，当第一次与外切时，求平移的时间.

Answer 1

【答案】（1）直线的解析式为：.（2）平移的时间为5秒.

【解析】

（1）求直线的解析式，可以先求出A、C两点的坐标，就可以根据待定系数法求出函数的解析式．

（2）设⊙O2平移t秒后到⊙O3处与⊙O1第一次外切于点P，⊙O3与x轴相切于D1点，连接O1O3，O3D1．

在直角△O1O3D1中，根据勾股定理，就可以求出O1D1，进而求出D1D的长，得到平移的时间．

（1）由题意得，

∴点坐标为.

∵在中，，

，

∴点的坐标为.

设直线的解析式为，

由过、两点，

得，

解得，

∴直线的解析式为：.

（2）如图，

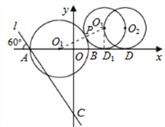
设平移秒后到处与第一次外切于点，

与轴相切于点，连接，.

则，

∵轴，∴，

在中，.

∵，

∴，

∴（秒），

∴平移的时间为5秒.