题目内容
如图1,抛物线C1:y=ax2+bx+2与直线AB:y=
x+
交于x轴上的一点A,和另一点B(3,n).

(1)求抛物线C1的解析式;
(2)点P是抛物线C1上的一个动点(点P在A,B两点之间,但不包括A,B两点),PM⊥AB于点M,PN∥y轴交AB于点N,在点P的运动过程中,存在某一位置,使得△PMN的周长最大,求此时P点的坐标,并求△PMN周长的最大值;
(3)如图2,将抛物线C1绕顶点旋转180°后,再作适当平移得到抛物线C2,已知抛物线C2的顶点E在第四象限的抛物线C1上,且抛物线C2与抛物线C1交于点D,过D点作x轴的平行线交抛物线C2于点F,过E点作x轴的平行线交抛物线C1于点G,是否存在这样的抛物线C2,使得四边形DFEG为菱形?若存在,请求E点的横坐标;若不存在请说明理由.
| 1 |
| 2 |
| 1 |
| 2 |

(1)求抛物线C1的解析式;
(2)点P是抛物线C1上的一个动点(点P在A,B两点之间,但不包括A,B两点),PM⊥AB于点M,PN∥y轴交AB于点N,在点P的运动过程中,存在某一位置,使得△PMN的周长最大,求此时P点的坐标,并求△PMN周长的最大值;
(3)如图2,将抛物线C1绕顶点旋转180°后,再作适当平移得到抛物线C2,已知抛物线C2的顶点E在第四象限的抛物线C1上,且抛物线C2与抛物线C1交于点D,过D点作x轴的平行线交抛物线C2于点F,过E点作x轴的平行线交抛物线C1于点G,是否存在这样的抛物线C2,使得四边形DFEG为菱形?若存在,请求E点的横坐标;若不存在请说明理由.
分析:(1)把点A(-1,0)、B(3,2)代入抛物线y=ax2+bx+2求出a、b的值,故可得出抛物线的解析式;
(2)设AB交y轴于D,故可得出D点坐标,由此可得出OA,OD,AD的长,进而求出△AOD的周长,再根据PN∥y轴,可知∠PNM=∠CDN=∠ADO,由相似三角形的判定定理得出Rt△ADO∽Rt△PNM,故可得出
=
,用PN表示出△PMN的周长,故可得出当PN取最大值时,C△PNM取最大值,设出PN两点的坐标,根据m的取值范围即可得出结论;
(3)设E(n,t),由题意得出抛物线C1,C2的解析式,再根据E在抛物线C1上可得出t的表达式,由四边形DFEG为菱形可知DF=FE=EG=DG,连接ED,由抛物线的对称性可知,ED=EF,故△DEG与△DEF均为正三角形,故D为抛物线C1的顶点,求出D点坐标,由DF∥x轴,且D、F关于直线x=n对称可得出DF的长,再根据△DEF为正三角形即可得出n的值,进而求出t的值,故可得出E点坐标.
(2)设AB交y轴于D,故可得出D点坐标,由此可得出OA,OD,AD的长,进而求出△AOD的周长,再根据PN∥y轴,可知∠PNM=∠CDN=∠ADO,由相似三角形的判定定理得出Rt△ADO∽Rt△PNM,故可得出
| C△PNM |
| C△AOD |
| PN |
| AD |
(3)设E(n,t),由题意得出抛物线C1,C2的解析式,再根据E在抛物线C1上可得出t的表达式,由四边形DFEG为菱形可知DF=FE=EG=DG,连接ED,由抛物线的对称性可知,ED=EF,故△DEG与△DEF均为正三角形,故D为抛物线C1的顶点,求出D点坐标,由DF∥x轴,且D、F关于直线x=n对称可得出DF的长,再根据△DEF为正三角形即可得出n的值,进而求出t的值,故可得出E点坐标.
解答:解:(1)∵A(-1,0)、B(3,2)在抛物线y=ax2+bx+2上,
∴
,
解得:
,
∴抛物线的解析式为y=-
x2+
x+2;
(2)∵设AB交y轴于D,则D(0,
),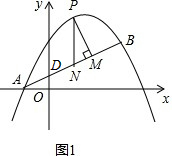 (如图1)
(如图1)
∴OA=1,OD=
,AD=
,
∴C△AOD=
,
∵PN∥y轴,
∴∠PNM=∠CDN=∠ADO,
∴Rt△ADO∽Rt△PNM.
∴
=
=
.
∴C△PNM=
×
PN=
PN.
∴当PN取最大值时,C△PNM取最大值.
设P(m,-
m2+
m+2)N(m,
m+
).则PN=-
m2+
m+2-(
m+
)=-
m2+m+
.
∵-1<m<3.
∴当m=1时,PN取最大值.
∴△PNM周长的最大值为
×2=
.此时P(1,3);
(3)设E(n,t),由题意得:抛物线C1为:y=-
(x-
)2+
,C2为:y=
(x-n)2+t.
∵E在抛物线C1上,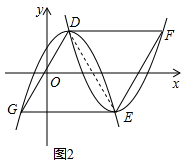
∴t=-
(n-
)2+
.
∵四边形DFEG为菱形.
∴DF=FE=EG=DG,
连接ED,由抛物线的对称性可知,ED=EF.
∴△DEG与△DEF均为正三角形.
∴D为抛物线C1的顶点.
∴D(
,
).
∵DF∥x轴,且D、F关于直线x=n对称.
∴DF=2(n-
).
∵DEF为正三角形.
∴
-[-
(n-
)2+
]=
×2(n-
),
解得:n=
.
∴t=-
.
∴存在点E,坐标为E(
,-
).
∴
|
解得:
|
∴抛物线的解析式为y=-
| 1 |
| 2 |
| 3 |
| 2 |
(2)∵设AB交y轴于D,则D(0,
| 1 |
| 2 |
 (如图1)
(如图1)∴OA=1,OD=
| 1 |
| 2 |
| ||
| 2 |
∴C△AOD=
3+
| ||
| 2 |
∵PN∥y轴,
∴∠PNM=∠CDN=∠ADO,
∴Rt△ADO∽Rt△PNM.
∴
| C△PNM |
| C△AOD |
| PN |
| AD |
5
| ||
| 5 |
∴C△PNM=
2
| ||
| 5 |
3+
| ||
| 2 |
5+3
| ||
| 5 |
∴当PN取最大值时,C△PNM取最大值.
设P(m,-
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∵-1<m<3.
∴当m=1时,PN取最大值.
∴△PNM周长的最大值为
5+3
| ||
| 5 |
10+6
| ||
| 5 |
(3)设E(n,t),由题意得:抛物线C1为:y=-
| 1 |
| 2 |
| 3 |
| 2 |
| 25 |
| 8 |
| 1 |
| 2 |
∵E在抛物线C1上,

∴t=-
| 1 |
| 2 |
| 3 |
| 2 |
| 25 |
| 8 |
∵四边形DFEG为菱形.
∴DF=FE=EG=DG,
连接ED,由抛物线的对称性可知,ED=EF.
∴△DEG与△DEF均为正三角形.
∴D为抛物线C1的顶点.
∴D(
| 3 |
| 2 |
| 25 |
| 8 |
∵DF∥x轴,且D、F关于直线x=n对称.
∴DF=2(n-
| 3 |
| 2 |
∵DEF为正三角形.
∴
| 25 |
| 8 |
| 1 |
| 2 |
| 3 |
| 2 |
| 25 |
| 8 |
| ||
| 2 |
| 3 |
| 2 |
解得:n=
3+4
| ||
| 2 |
∴t=-
| 23 |
| 8 |
∴存在点E,坐标为E(
3+4
| ||
| 2 |
| 23 |
| 8 |
点评:本题考查的是二次函数综合题,涉及到用待定系数法求二次函数的解析式、菱形的性质、等边三角形的判定与性质等相关知识,难度较大.

练习册系列答案
相关题目

 过C2顶点M的直线为l,且l与x轴交于点N.
过C2顶点M的直线为l,且l与x轴交于点N.
