��Ŀ����
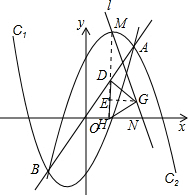
��ͼ����������C1��y=a��x+1��2-5��C2��y=-a��x-1��2+5��C1��C2�Ľ���ΪA��B����A�������ǣ�2��4������B�ĺ�������-2����1����a��ֵ����B�����ꣻ
��2����D���߶�AB�ϣ���D��x��Ĵ��ߣ�����Ϊ��H����DH���Ҳ�����������DHG����
 ��C2����M��ֱ��Ϊl����l��x�ύ�ڵ�N��
��C2����M��ֱ��Ϊl����l��x�ύ�ڵ�N������l����DHG�Ķ���G����D������Ϊ��1��2�������N�ĺ����ꣻ
����l���DHG�ı�DG�ཻ�����N�ĺ������ȡֵ��Χ��
��������1����������������ͬʱ����A��B���㣬��A��������������������У�������ô���ϵ����ֵ�����������B������꣮
��2������֪�˵�D�����꣬�����������DGH�ı߳�����G��GE��DH��E�������DE��EH��EG�ij������ݣ�1��������õ�C2�Ľ���ʽ�����������M�����꣬Ҳ���ܵõ�ME��MH�ij�����֤��MEG�ס�MHN�������������������ñ����߶Σ��������N��ĺ����꣮
�����N�������ȡֵ��Χ���迼��N������������С���������
�ٵ���D��A�غϣ���ֱ��l������Gʱ��N��ĺ�������ⷨ�ɲ��գ�2����˼·������G��GQ��x����Q������M��MF��x����F�������N�ĺ����꣬Ȼ��ֱ��ʾ��NQ��NF�ij���ͨ��֤��NQG�ס�NFM���������ñ����߶Σ�������ô�ʱN��ĺ����ꣻ
�ڵ���D��B�غϣ�ֱ��l����Dʱ��N��ĺ�������С���ⷨͬ�٣�
��2������֪�˵�D�����꣬�����������DGH�ı߳�����G��GE��DH��E�������DE��EH��EG�ij������ݣ�1��������õ�C2�Ľ���ʽ�����������M�����꣬Ҳ���ܵõ�ME��MH�ij�����֤��MEG�ס�MHN�������������������ñ����߶Σ��������N��ĺ����꣮
�����N�������ȡֵ��Χ���迼��N������������С���������
�ٵ���D��A�غϣ���ֱ��l������Gʱ��N��ĺ�������ⷨ�ɲ��գ�2����˼·������G��GQ��x����Q������M��MF��x����F�������N�ĺ����꣬Ȼ��ֱ��ʾ��NQ��NF�ij���ͨ��֤��NQG�ס�NFM���������ñ����߶Σ�������ô�ʱN��ĺ����ꣻ
�ڵ���D��B�غϣ�ֱ��l����Dʱ��N��ĺ�������С���ⷨͬ�٣�
��� �⣺��1���ߵ�A��2��4����������C1�ϣ�
�⣺��1���ߵ�A��2��4����������C1�ϣ�
��ѵ�A�������y=a��x+1��2-5��a=1��
��������C1�Ľ���ʽΪy=x2+2x-4��
��B��-2��b����
��b=-4��
��B��-2��-4����
��2������ͼ
��M��1��5����D��1��2������DH��x�ᣬ
���M��DH�ϣ�MH=5��
����G��GE��DH������ΪE��
�ɡ�DHG���������Σ��ɵ�EG=
��EH=1��
��ME=4��
��N��x��0������NH=x-1��
�ɡ�MEG�ס�MHN����
=
��
��
=
��
��x=
+1��
���N�ĺ�����Ϊ
+1��
�ڵ���D�Ƶ����A�غ�ʱ����ͼ��
ֱ��l��DG���ڵ�G����ʱ��N�ĺ��������
����G��M��x��Ĵ��ߣ�����ֱ�Ϊ��Q��F��
��N��x��0����
��A��2��4������AH=4���ҡ�AGHΪ�ȱ������Σ�
���AHG=60�㣬HG=AH=4��
���GHQ=30�㣬�֡�GQH=90�㣬
��GQ=
HG=2��HQ=
=2
��
��OQ=OH+HQ=2+2
��
��G��2+2
��2����
��NQ=x-2-2
��NF=x-1��GQ=2��MF=5��
�ߡ�NGQ�ס�NMF��
��
=
��
��
=
��
��x=
��
����D�Ƶ����B�غ�ʱ����ͼ��
ֱ��l��DG���ڵ�D������B��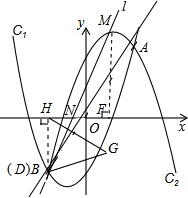
��ʱ��N�ĺ�������С��
��B��-2��-4����
��H��-2��0����D��-2��-4����
��N��x��0����
�ߡ�BHN�ס�MFN��
��
=
��
��
=
��
��x=-
��
���N������ķ�ΧΪ-
��x��
��x��0��
 �⣺��1���ߵ�A��2��4����������C1�ϣ�
�⣺��1���ߵ�A��2��4����������C1�ϣ���ѵ�A�������y=a��x+1��2-5��a=1��
��������C1�Ľ���ʽΪy=x2+2x-4��
��B��-2��b����
��b=-4��
��B��-2��-4����
��2������ͼ
��M��1��5����D��1��2������DH��x�ᣬ
���M��DH�ϣ�MH=5��
����G��GE��DH������ΪE��
�ɡ�DHG���������Σ��ɵ�EG=
| 3 |
��ME=4��
��N��x��0������NH=x-1��
�ɡ�MEG�ס�MHN����
| ME |
| MH |
| EG |
| HN |
��
| 4 |
| 5 |
| ||
| x-1 |
��x=
| 5 |
| 4 |
| 3 |
���N�ĺ�����Ϊ
| 5 |
| 4 |
| 3 |
�ڵ���D�Ƶ����A�غ�ʱ����ͼ��

ֱ��l��DG���ڵ�G����ʱ��N�ĺ��������
����G��M��x��Ĵ��ߣ�����ֱ�Ϊ��Q��F��
��N��x��0����
��A��2��4������AH=4���ҡ�AGHΪ�ȱ������Σ�
���AHG=60�㣬HG=AH=4��
���GHQ=30�㣬�֡�GQH=90�㣬
��GQ=
| 1 |
| 2 |
| 42-22 |
| 3 |
��OQ=OH+HQ=2+2
| 3 |
��G��2+2
| 3 |
��NQ=x-2-2
| 3 |
�ߡ�NGQ�ס�NMF��
��
| NQ |
| NF |
| GQ |
| MF |
��
x-2-2
| ||
| x-1 |
| 2 |
| 5 |
��x=
10
| ||
| 3 |
����D�Ƶ����B�غ�ʱ����ͼ��
ֱ��l��DG���ڵ�D������B��

��ʱ��N�ĺ�������С��
��B��-2��-4����
��H��-2��0����D��-2��-4����
��N��x��0����
�ߡ�BHN�ס�MFN��
��
| NH |
| FN |
| BH |
| MF |
��
| x+2 |
| 1-x |
| 4 |
| 5 |
��x=-
| 2 |
| 3 |
���N������ķ�ΧΪ-
| 2 |
| 3 |
10
| ||
| 3 |
�����������Ƕ��κ������ۺ��⣬��Ҫ������κ�������ʽ��ȷ�����ȱ������ε������Լ����������ε��ж������ʣ��ڽ��2����ʱ���ؼ�����ȷ����ͼ���������������ص����������Σ�Ȼ���������������ε���������⣮

��ϰ��ϵ�д�
�����Ŀ



