��Ŀ����
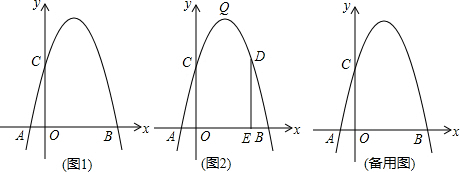
��֪����ͼ1��������C1��y=
(x-m)2+n��m��0���Ķ���ΪA����y���ཻ�ڵ�B��������C2��y=-
(x+m)2-n�Ķ���ΪC������y���ཻ�ڵ�D�����е�A��B��C��D�е��������㶼����ͬһ��ֱ��
��1���ж��ı���ABCD����״����˵�����ɣ�
��2����ͼ2����������y=
(x-m)2+n ��m��0���Ķ���A����x����ʱ���ı���ABCDǡ���������Σ�����ȷ��m��n��ֵ��
��3���Ƿ����m��n��ֵ��ʹ�ı���ABCD���ڱ�֮��Ϊ1��
�ľ��Σ������ڣ������m��n��ֵ���������ڣ���˵�����ɣ�
| 1 |
| 3 |
| 1 |
| 3 |

��1���ж��ı���ABCD����״����˵�����ɣ�
��2����ͼ2����������y=
| 1 |
| 3 |
��3���Ƿ����m��n��ֵ��ʹ�ı���ABCD���ڱ�֮��Ϊ1��
| 3 |
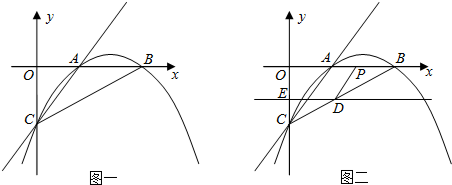
��������1��������Ŀ�������Ա�ʾ��A��m��n ����C��-m��-n �����������AO=CO����x=ʱ���������B��D�����꣬�Ӷ�����֤��BO=DO��CO�Ӷ��ó����ۣ�
��2����������y=
(x-m)2+n ��m��0���Ķ���A����x���ϣ����Եó�n=0�����ı���ABCDǡ���������Σ��������ε����ʾͿ��Եó�OA=OB������������ϵ�����m��ֵ��
��3�����ı���ABCD�Ǿ��Σ��ɾ��ε����ʿ��Եó�OA=OB�Ӷ�����һ��������ϵ���ɾ���ABCD���ڱ�֮��Ϊ1��
�����Եó�����ABO=60����ABO=30�㣬��AH��BD����ʾ��BH����OB=BH+OH�ڽ���һ����ʽ���Ӷ����ɷ����飬������������������Ľ�Ϳ����ˣ�
��2����������y=
| 1 |
| 3 |
��3�����ı���ABCD�Ǿ��Σ��ɾ��ε����ʿ��Եó�OA=OB�Ӷ�����һ��������ϵ���ɾ���ABCD���ڱ�֮��Ϊ1��
| 3 |
����⣺��1���ı���ABCD��ƽ���ı��Σ�
��A��m��n ����C��-m��-n ����
���A���C����ԭ��Գƣ�
���O��A��C������ͬһ��ֱ���ϣ�
��OA=OC��
��B(0��
m2+n)��D(0��-
m2-n)��
��OB=OD��
���ı���ABCD��ƽ���ı��Σ�
��2����������y=
(x-m)2+n(m��0)�Ķ���A����x���ϣ�
��n=0��
���ı���ABCD�������Σ�
��OA=OB����
m2=m��
��ã�m1=0���������⣬��ȥ����m2=3��
��ʱ�ı���ABCD��������
��m=3��n=0��
��3�����ı���ABCD�Ǿ��Σ�
��OA=OB����(
m2+n)2=m2+n2��
����ã�
m4+
m2n=m2
��m��0��
��m2+6n=9
�֡߾��ε��ڱ�֮��Ϊ1��
��
��AB��AD=1��
ʱ����ABO=60�㣬
����A��AH��BD��H����BH=
m��
��
m+n=
m2+n��
��
��
��ã�
��AD��AB=1��
ʱ����ABO=30�㣬
����A��AH��BD��H����BH=
m��
��
��
��ã�
��
�𣺴���m=
��n=1��m=3
��n=-3ʹ�ı���ABCD���ڱ�֮��Ϊ1��
�ľ��Σ�
��A��m��n ����C��-m��-n ����
���A���C����ԭ��Գƣ�
���O��A��C������ͬһ��ֱ���ϣ�
��OA=OC��
��B(0��
| 1 |
| 3 |
| 1 |
| 3 |
��OB=OD��
���ı���ABCD��ƽ���ı��Σ�
��2����������y=
| 1 |
| 3 |
��n=0��
���ı���ABCD�������Σ�
��OA=OB����
| 1 |
| 3 |
��ã�m1=0���������⣬��ȥ����m2=3��
��ʱ�ı���ABCD��������
��m=3��n=0��
��3�����ı���ABCD�Ǿ��Σ�
��OA=OB����(
| 1 |
| 3 |
����ã�
| 1 |
| 9 |
| 2 |
| 3 |

��m��0��
��m2+6n=9
�֡߾��ε��ڱ�֮��Ϊ1��
| 3 |
��AB��AD=1��
| 3 |
����A��AH��BD��H����BH=
| ||
| 3 |
��
| ||
| 3 |
| 1 |
| 3 |
��
|
��ã�
|
��AD��AB=1��
| 3 |
����A��AH��BD��H����BH=
| 3 |
��
|
��ã�
|
�𣺴���m=
| 3 |
| 3 |
| 3 |
������������һ�����κ������ۺ����⣬������ƽ���ı��ε��ж��������ε����ʵ����ã����ε����ʵ����ü����Ǻ���ֵ�����ã�

��ϰ��ϵ�д�
�����Ŀ