题目内容
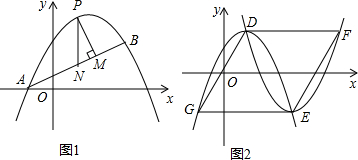
如图1,抛物线C1:y=-x2+4x-2与x轴交于A、B,直线l:y=-
x+b分别交x轴、y轴于S点和C点,抛物线C1的顶点E在直线l上.
(1)求直线l的解析式;
(2)如图2,将抛物线C1沿射线ES的方向平移得到抛物线C2,抛物线C2的顶点F在直线l上,并交x轴于M、N两点,且tan∠EAB=
•tan∠FNM,求抛物线C1平移的距离;
(3)将抛物线C2沿水平方向平移得到抛物线C3,抛物线C3与x轴交于P、G两点(点P在点G的左侧),使得△PEF为直角三角形,求抛物线C3的解析式.

| 1 |
| 2 |
(1)求直线l的解析式;
(2)如图2,将抛物线C1沿射线ES的方向平移得到抛物线C2,抛物线C2的顶点F在直线l上,并交x轴于M、N两点,且tan∠EAB=
| 2 |
(3)将抛物线C2沿水平方向平移得到抛物线C3,抛物线C3与x轴交于P、G两点(点P在点G的左侧),使得△PEF为直角三角形,求抛物线C3的解析式.

分析:(1)利用配方法能得到抛物线C1的顶点坐标,代入直线l的解析式后即可得解.
(2)由于抛物线C2是由抛物线C1沿射线CS平移所得,所以C2的顶点F仍在直线l上,且抛物线C2的解析式中二次项系数不变(代表的是抛物线的开口方向和大小),首先根据点E的坐标求出tan∠EAM的值,代入题干给出的关系式后可得tan∠FNM的值,然后根据直线l的解析式设出点F的坐标,进而由tan∠FNM的值表示出点M或点N的坐标,再代入抛物线C2的解析式中后即可得到点F的坐标,E、F两点坐标已知,其距离可求.
(3)抛物线C2沿水平方向平移时,与x轴交点间的距离不变,顶点纵坐标不变,可先设出点P、G以及C3顶点的坐标,那么线段EF、EP、FP的长度表达式可得,若△PEF是直角三角形,那么这三边的长必满足勾股定理,然后分点E、F、P分别是直角顶点列出等式求解.
(2)由于抛物线C2是由抛物线C1沿射线CS平移所得,所以C2的顶点F仍在直线l上,且抛物线C2的解析式中二次项系数不变(代表的是抛物线的开口方向和大小),首先根据点E的坐标求出tan∠EAM的值,代入题干给出的关系式后可得tan∠FNM的值,然后根据直线l的解析式设出点F的坐标,进而由tan∠FNM的值表示出点M或点N的坐标,再代入抛物线C2的解析式中后即可得到点F的坐标,E、F两点坐标已知,其距离可求.
(3)抛物线C2沿水平方向平移时,与x轴交点间的距离不变,顶点纵坐标不变,可先设出点P、G以及C3顶点的坐标,那么线段EF、EP、FP的长度表达式可得,若△PEF是直角三角形,那么这三边的长必满足勾股定理,然后分点E、F、P分别是直角顶点列出等式求解.
解答:解:(1)∵抛物线C1:y=-x2+4x-2=-(x-2)2+2,
∴顶点E(2,2),代入直线l的解析式后,得:
-
×2+b=2,b=3
∴直线l:y=-
x+3.
(2)∵顶点F在直线l上,
∴可以设顶点F(m,-
m+3),
∴抛物线C2可表示为 y=-(x-m)2-
m+3;
∵A(2-
,0)、B(2+
,0),E(2,2)
∴tan∠EAB=
=
;
∵tan∠EAB=
•tan∠FNM,∴tan∠FNM=1,∠FNM=45°
∴ON=m+(-
m+3)=
m+3,即 N(
m+3,0)
代入y=-(x-m)2-
m+3中,得 m=4,即 F(4,1);
∴EF=
=
,即抛物线C1平移的距离EF=
.
(3)由(2)知 C2:y=-(x-4)2+1,∴M(3,0)、N(5,0);
∵将抛物线C2沿水平方向平移得到抛物线C3,∴PG=MN=2,
设P(p,0),则Q(p+2,0),抛物线C3顶点(p+1,1)、抛物线C3:y=-(x-p-1)2+1;
∵E(2,2)、F(4,1),
∴PE2=(p-2)2+22=p2-4p+8;PF2=(p-4)2+12=p2-8p+17,EF2=5;
①当∠PEF=90°时,p2-4p+8+5=p2-8p+17,∴p=1,此时C3为 y=-(x-2)2+1;
②当∠PFE=90°时,p2-8p+17+5=p2-4p+8,∴p=
,此时C3为 y=-(x-
)2+1;
③当∠EPF=90°时,p2-8p+17+p2-4p+8=5,即 p2-6p+10=0,△<0,此时C3不存在;
∴抛物线C3的解析式为 y=-(x-2)2+1或y=-(x-
)2+1.
∴顶点E(2,2),代入直线l的解析式后,得:
-
| 1 |
| 2 |
∴直线l:y=-
| 1 |
| 2 |
(2)∵顶点F在直线l上,
∴可以设顶点F(m,-
| 1 |
| 2 |
∴抛物线C2可表示为 y=-(x-m)2-
| 1 |
| 2 |
∵A(2-
| 2 |
| 2 |
∴tan∠EAB=
| 2 | ||
2-(2-
|
| 2 |
∵tan∠EAB=
| 2 |
∴ON=m+(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
代入y=-(x-m)2-
| 1 |
| 2 |
∴EF=
| (4-2)2+(1-2)2 |
| 5 |
| 5 |
(3)由(2)知 C2:y=-(x-4)2+1,∴M(3,0)、N(5,0);
∵将抛物线C2沿水平方向平移得到抛物线C3,∴PG=MN=2,
设P(p,0),则Q(p+2,0),抛物线C3顶点(p+1,1)、抛物线C3:y=-(x-p-1)2+1;
∵E(2,2)、F(4,1),
∴PE2=(p-2)2+22=p2-4p+8;PF2=(p-4)2+12=p2-8p+17,EF2=5;
①当∠PEF=90°时,p2-4p+8+5=p2-8p+17,∴p=1,此时C3为 y=-(x-2)2+1;
②当∠PFE=90°时,p2-8p+17+5=p2-4p+8,∴p=
| 7 |
| 2 |
| 9 |
| 2 |
③当∠EPF=90°时,p2-8p+17+p2-4p+8=5,即 p2-6p+10=0,△<0,此时C3不存在;
∴抛物线C3的解析式为 y=-(x-2)2+1或y=-(x-
| 9 |
| 2 |
点评:此题主要考查了函数解析式的确定、函数图象的平移、解直角三角形的应用以及直角三角形的判定等知识;题(3)中,给出的直角三角形并没有明确说明它的直角顶点,因此一定要注意进行分类讨论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

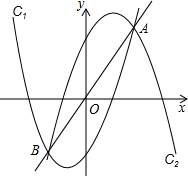 过C2顶点M的直线为l,且l与x轴交于点N.
过C2顶点M的直线为l,且l与x轴交于点N.