题目内容
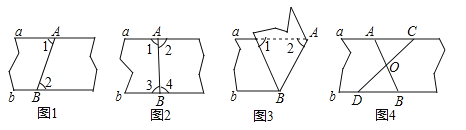
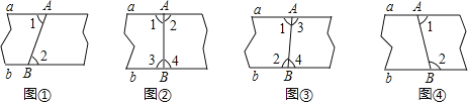
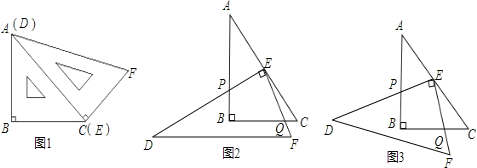
【题目】如图1,一副直角三角板满足AB=BC,AC=DE,∠ABC=∠DEF=90°,∠EDF=30°
操作:将三角板DEF的直角顶点E放置于三角板ABC的斜边AC上,再将三角板DEF绕点E旋转,并使边DE与边AB交于点P,边EF与边BC于点Q.
探究一:在旋转过程中,
(1)如图2,当![]() 时,EP与EQ满足怎样的数量关系?并给出证明;
时,EP与EQ满足怎样的数量关系?并给出证明;
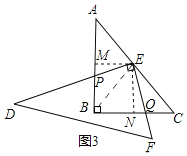
(2)如图3,当![]() 时,EP与EQ满足怎样的数量关系?并说明理由;
时,EP与EQ满足怎样的数量关系?并说明理由;
(3)根据你对(1)、(2)的探究结果,试写出当![]() 时,EP与EQ满足的数量关系式为 ,其中m的取值范围是 .(直接写出结论,不必证明)
时,EP与EQ满足的数量关系式为 ,其中m的取值范围是 .(直接写出结论,不必证明)
探究二:若![]() 且AC=30cm,连接PQ,设△EPQ的面积为S(cm2),在旋转过程中:
且AC=30cm,连接PQ,设△EPQ的面积为S(cm2),在旋转过程中:
(1)S是否存在最大值或最小值?若存在,求出最大值或最小值;若不存在,说明理由.
(2)随着S取不同的值,对应△EPQ的个数有哪些变化,求出相应S的值或取值范围.
【答案】探究一:(1)EP=EQ;证明见解析;(2)1:2,证明见解析;(3)EP:EQ=1:m,∴0<m≤2+![]() ;探究二:(1)当x=10
;探究二:(1)当x=10![]() 时,面积最小,是50cm2;当x=10
时,面积最小,是50cm2;当x=10![]() 时,面积最大,是75cm2.(2)50<S≤62.5时,这样的三角形有2个;当S=50或62.5<S≤75时,这样的三角形有一个.
时,面积最大,是75cm2.(2)50<S≤62.5时,这样的三角形有2个;当S=50或62.5<S≤75时,这样的三角形有一个.
【解析】探究一:(1)连接BE,根据已知条件得到E是AC的中点,根据等腰直角三角形的性质可以证明BE=CE,∠PBE=∠C,根据等角的余角相等可以证明∠BEP=∠CEQ,即可得到全等三角形,从而证明结论;
(2)作EM⊥AB,EN⊥BC于M、N,根据两个角对应相等证明△MEP∽△NWQ,发现EP:EQ=EM:EN,再根据等腰直角三角形的性质得到EM:EN=AE:CE;
(3)根据(2)中求解的过程,可以直接写出结果;要求m的取值范围,根据交点的位置的限制进行分析;
探究二:(1)设EQ=x,结合上述结论,用x表示出三角形的面积,根据x的最值求得面积的最值;
(2)首先求得EQ和EB重合时的三角形的面积的值,再进一步分情况讨论.
探究一:(1)连接BE,
根据E是AC的中点和等腰直角三角形的性质,得
BE=CE,∠PBE=∠C,
又∠BEP=∠CEQ,
则△BEP≌△CEQ,得EP=EQ;
(2)作EM⊥AB,EN⊥BC于M,N,
∴∠EMP=∠ENC,
∵∠MEP+∠PEN=∠PEN+∠NEF=90°,
∴∠MEP=∠NEF,
∴△MEP∽△NEQ,
∴EP:EQ=EM:EN=AE:CE=1:2;
(3)过E点作EM⊥AB于点M,作EN⊥BC于点N,
∵在四边形PEQB中,∠B=∠PEQ=90°,
∴∠EPB+∠EQB=180°(四边形的内角和是360°),
又∵∠EPB+∠MPE=180°(平角是180°),
∴∠MPE=∠EQN(等量代换),
∴Rt△MEP∽Rt△NEQ,
∴![]() ,
,
在Rt△AME∽Rt△ENC,
∴![]() ,
,
∴![]() ,
,
EP与EQ满足的数量关系式为EP:EQ=1:m,
∴0<m≤2+![]() ;(当m>2+
;(当m>2+![]() 时,EF与BC不会相交).
时,EF与BC不会相交).
探究二:若AC=30cm,
(1)设EQ=x,则S=![]() x2,
x2,
所以当x=10![]() 时,面积最小,是50cm2;
时,面积最小,是50cm2;
当x=10![]() 时,面积最大,是75cm2;
时,面积最大,是75cm2;
(2)当x=EB=5![]() 时,S=62.5cm2,
时,S=62.5cm2,
故当50<S≤62.5时,这样的三角形有2个;
当S=50或62.5<S≤75时,这样的三角形有一个.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案【题目】甲、乙两名同学分别进行6次射击训练,训练成绩(单位:环)如下表
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六交 | |
甲 | 9 | 8 | 6 | 7 | 8 | 10 |
乙 | 8 | 7 | 9 | 7 | 8 | 8 |
对他们的训练成绩作如下分析,其中说法正确的是( )
A. 他们训练成绩的平均数相同 B. 他们训练成绩的中位数不同
C. 他们训练成绩的众数不同 D. 他们训练成绩的方差不同
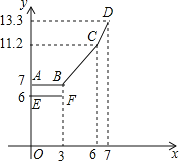
【题目】为缓解油价上涨给出租车待业带来的成本压力,某巿自2018年11月17日起,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数)
行驶路程 | 收费标准 | |
调价前 | 调价后 | |
不超过3km的部分 | 起步价6元 | 起步价a 元 |
超过3km不超出6km的部分 | 每公里2.1元 | 每公里b元 |
超出6km的部分 | 每公里c元 | |
设行驶路程xkm时,调价前的运价y1(元),调价后的运价为y2(元)如图,折线ABCD表示y2与x之间的函数关系式,线段EF表示当0≤x≤3时,y1与x的函数关系式,根据图表信息,完成下列各题:
(1)填空:a= ,b= ,c= .
(2)写出当x>3时,y1与x的关系,并在上图中画出该函数的图象.
(3)函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义,若不存在请说明理由.