题目内容
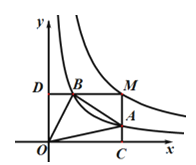
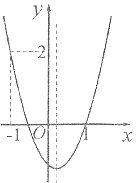
【题目】如图，二次函数
的图象开口向上，图象经过点(-1，2)和(1，0)，且与
轴相交于负半轴，下列结论：①
；②方程
的两根一个大于1，另一个小于-1；③
；④
.其中正确结论的个数是( )
A. 1个B. 2个C. 3个D. 4个
【答案】D
【解析】
由抛物线开口向上可得a>0，根据对称轴在y轴右侧，且小于1，可对①进行判断；根据抛物线y=ax2+bx+c-3是抛物线y=ax2+bx+c的图象向下平移3个单位，可对②进行判断；根据二次函数图象上点的坐标特征得到a-b+c=2，a+b+c=0，可对③进行判断；由③可求出a+c的值，几何c<0可对④进行判断，综上即可得答案.
∵对称轴在y轴右侧，且小于1，
∴
<1，
∴2a+b>0，故①正确，
∵抛物线y=ax2+bx+c-3是抛物线y=ax2+bx+c的图象向下平移3个单位，抛物线y=ax2+bx+c-3经过点，（1，0）
∴方程ax2+bx+c-3=0有一个根大于1，
∵抛物线y=ax2+bx+c向下平移2个单位时与x轴的交点为（-1，0），
∴方程ax2+bx+c-3=0的另一个根小于-1，故②正确
∵抛物线y=ax2+bx+c的图象开口向上，
∴a>0，
∵抛物线y=ax2+bx+c的图象经过点（-1，2）和（1，0），
∴
，
解得：
，故③正确，
∵抛物线y轴相交于负半轴，
∴c<0，
∵a+c=1，
∴a>1，故④正确，
综上所述：正确结论有①②③④共4个，
故选D.
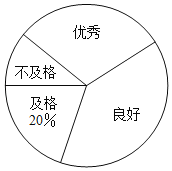
【题目】某校为了解八年级男生“立定跳远”成绩的情况，随机选取该年级部分男生进行测试，以下是根据测试成绩绘制的统计图表的一部分．
成绩等级 | 频数（人） | 频率 |
优秀 | 15 | 0.3 |
良好 | ||
及格 | ||
不及格 | 5 |
根据以上信息，解答下列问题
（1）被测试男生中，成绩等级为“优秀”的男生人数为 人，成绩等级为“及格”的男生人数占被测试男生总人数的百分比为 %；
（2）被测试男生的总人数为 人，成绩等级为“不及格”的男生人数占被测试男生总人数的百分比为 %；
（3）若该校八年级共有180名男生，根据调查结果，估计该校八年级男生成绩等级为“良好”的学生人数．
