题目内容
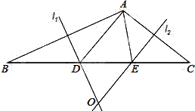
【题目】如图，在等边△ABC中，AB=4，点P是BC边上的动点，点P关于直线AB，AC的对称点分别为M，N，则线段MN长的取值范围是 ． 
【答案】6≤MN≤4 
【解析】解：（解法一）如图1，当点P为BC的中点时，MN最短． 此时E、F分别为AB、AC的中点，
∴PE= 
AC，PF= AB，EF= BC，
∴MN=ME+EF+FN=PE+EF+PF=6；
如图2，当点P和点B（或点C）重合时，此时BN（或CM）最长．
此时G（H）为AB（AC）的中点，
∴CG=2 （BH=2 ），
CM=4 （BN=4 ）．
故线段MN长的取值范围是6≤MN≤4 ．
故答案为：6≤MN≤4 ．
（解法二）连接PM交AB于点E，连接PN交AC于点F，过点M作MD⊥PN于点D，如图3所示．
设BP=x（0≤x≤4），则PE= 
x，CP=4﹣x，PF= （4﹣x），
∴PM= x，PN= （4﹣x）．
∵∠B=∠C=60°，
∴∠BPE=∠CPF=30°，
∴∠MPD=∠BPE+∠BPD=∠BPE+∠CPF=60°，
∴DP= PM= x，MD= PM= 
x．
在Rt△MDN中，MD= x，ND=PN+PD= （4﹣x）+ x= （8﹣x），
∴MN2=MD2+ND2=3（x﹣2）2+36，
∴当x=2时，MN取最小值6；当x=0或x=4时，MN取最大值4 ．
故答案为：6≤MN≤4 ．
（解法三）连接AM、AN、AP，过点A作AD⊥MN于点D，如图所示．
∵点P关于直线AB，AC的对称点分别为M，N，
∴AM=AP=AN，∠MAB=∠PAB，∠NAC=∠PAC，
∴△MAN为顶角为120°的等腰三角形，
∴∠AMD=30°，
∴AD= AM，MD= AM，MN= AM．
∵AM=AP，2 ≤AP≤4，
∴6≤MN≤4 ．
故答案为：6≤MN≤4 ．
（方法一）当点P为BC的中点时，MN最短，求出此时MN的长度，当点P与点B（或C）重合时，BN（或CM）最长，求出此时BN（或CM）的长度，由此即可得出MN的取值范围．
（方法二）连接PM交AB于点E，连接PN交AC于点F，过点M作MD⊥PN于点D，设BP=x（0≤x≤4），则PE= x，CP=4﹣x，PF= （4﹣x），根据等边三角形的性质结合轴对称的性质即可得出PM、PN的长度，由角的计算可得出∠MPD=60°，进而可得出MD、PD的长度，在Rt△MDN中，利用勾股定理即可得出MN2=MD2+ND2=3（x﹣2）2+36，再根据二次函数的性质即可解决最值问题．
（方法三）连接AM、AN、AP，过点A作AD⊥MN于点D，由对称性可知AM=AP=AN、△MAN为顶角为120°的等腰三角形，进而即可得出MN= AP，再根据AP的取值范围即可得出线段MN长的取值范围．
