题目内容
【题目】已知直线l1：y=kx﹣4的图象与直线l2：y=
x+1的图象平行．
（1）求直线l1的图象与x轴，y轴所围成图形的面积；
（2）求原点到直线l1的距离．
【答案】（1）6；（2）
．
【解析】
（1）根据平行得出k=
，求出与想、y轴的交点坐标，即可求出面积；
（2）根据垂直求出a的值，求出组成的方程组的解，即可求出答案．
解：（1）∵直线l1：y=kx﹣4的图象与直线l2：y=x+1的图象平行，
∴k=，
即直线l1：y=x﹣4，
当x=0时，y=﹣4，
当y=0时，x=3，
所以直线l1的图象与x轴，y轴所围成图形的面积是
=6；
（2）设过原点且垂直于直线l1的直线的解析式为y=ax，
则a=﹣1，
解得：a=﹣，
即y=﹣x，
解方程组
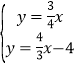得：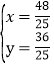
，
= ，
即原点到直线l1的距离是 ．
练习册系列答案
阅读快车系列答案
相关题目
