题目内容
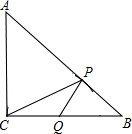
 16、已知△ABC中,∠C=90°,沿过B的一条直线BE折叠这个三角形,使点C与AB边上的一点D重合,如图所示.
16、已知△ABC中,∠C=90°,沿过B的一条直线BE折叠这个三角形,使点C与AB边上的一点D重合,如图所示.(1)要使D恰为AB的中点,还应添加一个什么条件?(请写出一个你认为正确的添加条件)
(2)将(1)中的添加条件作为题目的补充条件,试说明其能使D为AB中点的理由.
分析:根据直角三角形中特殊角度30度时的特殊性质可知:当∠A=30°时,D恰为AB的中点.利用轴对称的知识即可证明.
解答:解:(1)∠A=30°(答案不惟一);
证明:(2)∵∠A=30°,∠C=90°,
∴AB=2BC.
由已知C与D重合,
∴AB=2BC=2BD.
∴D为AB中点.
证明:(2)∵∠A=30°,∠C=90°,
∴AB=2BC.
由已知C与D重合,
∴AB=2BC=2BD.
∴D为AB中点.
点评:本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变.要掌握直角三角形中特殊角度30度时的特殊性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 情况;若不可能,请说明理由.
情况;若不可能,请说明理由.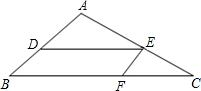 已知△ABC中,DE∥BC,EF∥AB,AB=3,BC=6,AD:DB=2:1,则四边形DBFE的周长为
已知△ABC中,DE∥BC,EF∥AB,AB=3,BC=6,AD:DB=2:1,则四边形DBFE的周长为 如图所示,已知△ABC中,AB=AC,以AB为直径作⊙O交BC于D,交AC于E,过D作DF⊥AC于F
如图所示,已知△ABC中,AB=AC,以AB为直径作⊙O交BC于D,交AC于E,过D作DF⊥AC于F 如图,已知△ABC中,AB=AC,AB垂直平分线交AC于D,连接BE,若∠A=40°,则∠EBC=( )
如图,已知△ABC中,AB=AC,AB垂直平分线交AC于D,连接BE,若∠A=40°,则∠EBC=( )