题目内容
【题目】如图,在直角梯形ABCD中,AD∥BC,∠B=90°,且AD=12cm,AB=8cm,DC=10cm,若动点P从A点出发,以每秒2cm的速度沿线段AD向点D运动;动点Q从C点出发以每秒3cm的速度沿CB向B点运动,当P点到达D点时,动点P、Q同时停止运动,设点P、Q同时出发,并运动了t秒,回答下列问题:
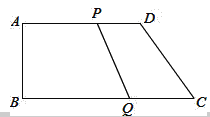
(1)BC= cm;
(2)当t为多少时,四边形PQCD成为平行四边形?
(3)当t为多少时,四边形PQCD为等腰梯形?
(4)是否存在t,使得△DQC是等腰三角形?若存在,请求出t的值;若不存在,说明理由.
【答案】(1)18;(2)当t=![]() 秒时四边形PQCD为平行四边形;(3)当t=
秒时四边形PQCD为平行四边形;(3)当t=![]() 时,四边形PQCD为等腰梯形;(4)存在t, t的值为
时,四边形PQCD为等腰梯形;(4)存在t, t的值为![]() 秒或4秒或
秒或4秒或![]() 秒.
秒.
【解析】试题分析:(1)作DE⊥BC于E,则四边形ABED为矩形.在直角△CDE中,已知DC、DE的长,根据勾股定理可以计算EC的长度,根据BC=BE+EC即可求出BC的长度;
(2)由于PD∥QC,所以当PD=QC时,四边形PQCD为平行四边形,根据PD=QC列出关于t的方程,解方程即可;
(3)首先过D作DE⊥BC于E,可求得EC的长,又由当PQ=CD时,四边形PQCD为等腰梯形,可求得当QC-PD=QC-EF=QF+EC=2CE,即3t-(12-2t)=12时,四边形PQCD为等腰梯形,解此方程即可求得答案;
(4)因为三边中,每两条边都有相等的可能,所以应考虑三种情况.结合路程=速度×时间求得其中的有关的边,运用等腰三角形的性质和解直角三角形的知识求解.
试题解析:根据题意得:PA=2t,CQ=3t,则PD=AD-PA=12-2t.
(1)如图,过D点作DE⊥BC于E,则四边形ABED为矩形,
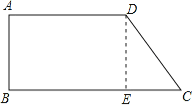
DE=AB=8cm,AD=BE=12cm,
在直角△CDE中,∵∠CED=90°,DC=10cm,DE=8cm,
∴EC=![]() =6cm,
=6cm,
∴BC=BE+EC=18cm.
(2)∵AD∥BC,即PD∥CQ,
∴当PD=CQ时,四边形PQCD为平行四边形,
即12-2t=3t,
解得t=![]() 秒,
秒,
故当t=![]() 秒时四边形PQCD为平行四边形;
秒时四边形PQCD为平行四边形;
(3)如图,过D点作DE⊥BC于E,则四边形ABED为矩形,DE=AB=8cm,AD=BE=12cm,
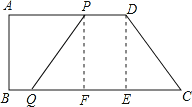
当PQ=CD时,四边形PQCD为等腰梯形.
过点P作PF⊥BC于点F,过点D作DE⊥BC于点E,则四边形PDEF是矩形,EF=PD=12-2t,PF=DE.
在Rt△PQF和Rt△CDE中,
![]() ,
,
∴Rt△PQF≌Rt△CDE(HL),
∴QF=CE,
∴QC-PD=QC-EF=QF+EC=2CE,
即3t-(12-2t)=12,
解得:t=![]() ,
,
即当t=![]() 时,四边形PQCD为等腰梯形;
时,四边形PQCD为等腰梯形;
(4)△DQC是等腰三角形时,分三种情况讨论:
①当QC=DC时,即3t=10,
∴t=![]() ;
;
②当DQ=DC时, ![]()
∴t=4;
③当QD=QC时,3t×![]()
∴t=![]() .
.
故存在t,使得△DQC是等腰三角形,此时t的值为![]() 秒或4秒或
秒或4秒或![]() 秒.
秒.

 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案