题目内容
27、若方程x2+px-p2=0的两根分别为x1、x2,且满足x1+x2=x1x2.
(1)试说明方程总有两个实数根;
(2)求P的值.
(1)试说明方程总有两个实数根;
(2)求P的值.
分析:(1)要说明方程总有两个实数根,即说明△≥0即可.
(2)根据根与系数的关系有:x1+x2=-p,x1x2=-p2,再根据x1+x2=x1x2得到p的方程,解方程即可.
(2)根据根与系数的关系有:x1+x2=-p,x1x2=-p2,再根据x1+x2=x1x2得到p的方程,解方程即可.
解答:解:(1)∵△=p2-4×1×(-p2)=5p2,
而5p2≥0,即△≥0,
所以方程总有两个实数根;
(2)∵x1+x2=-p,x1x2=-p2,
而x1+x2=x1x2,
∴-p=-p2,即p2-p=0,p(p-1)=0,
∴p=0或1.
而5p2≥0,即△≥0,
所以方程总有两个实数根;
(2)∵x1+x2=-p,x1x2=-p2,
而x1+x2=x1x2,
∴-p=-p2,即p2-p=0,p(p-1)=0,
∴p=0或1.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.同时考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根与系数的关系:x1+x2=-$frac{b}{a}$,x1x2=$frac{c}{a}$.

练习册系列答案
相关题目
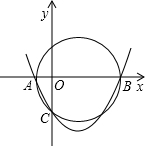 (1998•东城区)如图,在直角坐标系xoy中,A、B是x轴上两点,以AB为直径的圆交y轴于C点,设过A、B、C三点的抛物线解析式为y=x2-px+q,若方程x2-px+q=0两根的倒数和为-2
(1998•东城区)如图,在直角坐标系xoy中,A、B是x轴上两点,以AB为直径的圆交y轴于C点,设过A、B、C三点的抛物线解析式为y=x2-px+q,若方程x2-px+q=0两根的倒数和为-2