题目内容
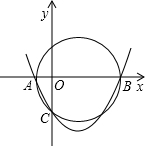（1998•东城区）如图，在直角坐标系xoy中，A、B是x轴上两点，以AB为直径的圆交y轴于C点，设过A、B、C三点的抛物线解析式为y=x2-px+q，若方程x2-px+q=0两根的倒数和为-2（1）求此抛物线的解析式；
（2）设平行于x轴的直线交该抛物线于E、F两点，问是否存在以线段EF为直径的圆恰好与x轴相切？若存在，求出此圆的圆心和半径；若不存在，说明理由．
分析：（1）由于AB是圆的直径，根据相交弦定理的推论可得OC2=OA•OB，若设A（x1，0），B（x2，0），那么q2=-x1x2，根据根与系数的关系知x1x2=q，联立两式即可求得q的值，根据韦达定理可求得方程的两根之和与两根之积，即可表示出它们的倒数和，已知了倒数和为2，即可求得p的值，由此确定抛物线的解析式；
（2）存在以线段EF为直径的圆恰好与x轴相切，理由为：求出抛物线的对称轴，设出圆的半径为|r|，根据对称轴得到E与F的坐标，将E坐标代入抛物线解析式求出r的值，进而确定出此时圆心坐标．
（2）存在以线段EF为直径的圆恰好与x轴相切，理由为：求出抛物线的对称轴，设出圆的半径为|r|，根据对称轴得到E与F的坐标，将E坐标代入抛物线解析式求出r的值，进而确定出此时圆心坐标．
解答：解：（1）由题意，设A（x1，0），B（x2，0），C（0，q），
∵OA=-x1，OB=x2，又CO⊥AB，
∴CO2=AO•OB，即q2=-x1x2；
又∵x1，x2是方程x2-px+q=0的两根，
∴x1•x2=q，
∴q2=-q，
∴q1=-1，q2=0（舍去），
∴q=-1，
∵x1，x2是方程x2-px+q=0的两根，
∴x1+x2=p，
又∵q=-1，
∴x1x2=-1，
∴
+
=
=
=
=-2，
∴p=2，
∴所求抛物线的关系式为y=x2-2x-1；
（2）存在，理由为：
抛物线的对称轴为直线x=1，
设满足题意圆的半径为|r|，可得出E（1+|r|，|r|）或F（1-|r|，|r|），
将E坐标代入抛物线得：|r|=（1+|r|）2-2（1+|r|）-1，
解得：|r|=2，
∴E（3，2），F（-1，2），
∴线段EF的中点坐标为（1，2），即为此时圆心坐标．
∵OA=-x1，OB=x2，又CO⊥AB，
∴CO2=AO•OB，即q2=-x1x2；
又∵x1，x2是方程x2-px+q=0的两根，
∴x1•x2=q，
∴q2=-q，
∴q1=-1，q2=0（舍去），
∴q=-1，
∵x1，x2是方程x2-px+q=0的两根，
∴x1+x2=p，
又∵q=-1，
∴x1x2=-1，
∴
| 1 |
| x1 |
| 1 |
| x2 |
| x1+x2 |
| x1x2 |
| p |
| q |
| p |
| -1 |
∴p=2，
∴所求抛物线的关系式为y=x2-2x-1；
（2）存在，理由为：
抛物线的对称轴为直线x=1，
设满足题意圆的半径为|r|，可得出E（1+|r|，|r|）或F（1-|r|，|r|），
将E坐标代入抛物线得：|r|=（1+|r|）2-2（1+|r|）-1，
解得：|r|=2，
∴E（3，2），F（-1，2），
∴线段EF的中点坐标为（1，2），即为此时圆心坐标．
点评：此题考查了二次函数综合题，涉及的知识有：相交弦定理，坐标与图形性质，根与系数的关系，二次函数的性质，是一道综合性较强的压轴题．
练习册系列答案
相关题目