题目内容
已知反比例函数的解析式为y=
(k≠1).
(1)在反比例函数图象的每一条曲线上,y随着x的增大而增大,求k的取值范围;
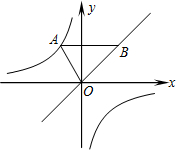
(2)在(1)的条件下点A为双曲线y=
(x<0)上一点,AB∥x轴交直线y=x于点B,若AB2-OA2=4,求反比例函数的解析式.

| 1-k |
| x |
(1)在反比例函数图象的每一条曲线上,y随着x的增大而增大,求k的取值范围;
(2)在(1)的条件下点A为双曲线y=
| 1-k |
| x |

(1)∵在双曲线的每个分支内,y随着x的增大而增大,
∴1-k<0,
∴k>1;
(2)点B在直线y=x上,设B(t,t),1-k=m(m≠0),
故双曲线解析式为y=
(m≠0),
∵AB∥x轴,
∴A点的纵坐标为t,
把y=t代入y=
得x=
,
∴A点坐标为(
,t),
∴AB2=(t-
)2,OA2=(
)2+t2,
∵AB2-OA2=4,
∴(t-
)2-[(
)2+t2]=4,解得:m=-2,
故1-k=-2,
∴反比例函数的解析式为y=
.
∴1-k<0,
∴k>1;
(2)点B在直线y=x上,设B(t,t),1-k=m(m≠0),
故双曲线解析式为y=
| m |
| x |
∵AB∥x轴,
∴A点的纵坐标为t,
把y=t代入y=
| m |
| x |
| m |
| t |
∴A点坐标为(
| m |
| t |
∴AB2=(t-
| m |
| t |
| m |
| t |
∵AB2-OA2=4,
∴(t-
| m |
| t |
| m |
| t |
故1-k=-2,
∴反比例函数的解析式为y=
| -2 |
| x |


练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案
相关题目

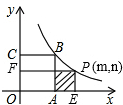
 y轴于点B.一次函数的图象分别交x轴、y轴于点C、D,且S△PBD=4,OC=OA.
y轴于点B.一次函数的图象分别交x轴、y轴于点C、D,且S△PBD=4,OC=OA.