题目内容
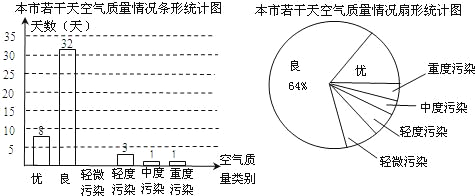
【题目】九（3）班为了组队参加学校举行的“五水共治”知识竞赛，在班里选取了若干名学生，分成人数相同的甲、乙两组，进行了四次“五水共治”模拟竞赛，成绩优秀的人数和优秀率分别绘制成如图统计图．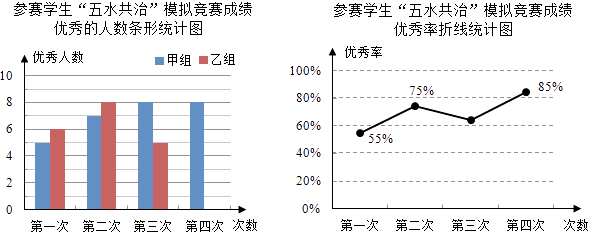 
根据统计图，解答下列问题：
（1）第三次成绩的优秀率是多少？并将条形统计图补充完整；
（2）已求得甲组成绩优秀人数的平均数 
=7，方差 
=1.5，请通过计算说明，哪一组成绩优秀的人数较稳定？
【答案】
（1）解：总人数：（5+6）÷55%=20（人），
第三次的优秀率：（8+5）÷20×100%=65%，
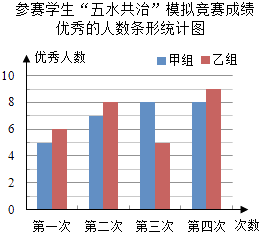
第四次乙组的优秀人数为：20×85%﹣8=17﹣8=9（人）．
补全条形统计图，如图所示：
（2）解： 
=（6+8+5+9）÷4=7，
S2乙组= 
×[（6﹣7）2+（8﹣7）2+（5﹣7）2+（9﹣7）2]=2.5，
S2甲组＜S2乙组，所以甲组成绩优秀的人数较稳定
【解析】（1）利用优秀率求得总人数，根据优秀率=优秀人数除以总人数计算；（2）先根据方差的定义求得乙班的方差，再根据方差越小成绩越稳定，进行判断．
练习册系列答案
黎明文化寒假作业系列答案
相关题目
