题目内容
【题目】(1)将两条宽度一样的矩形纸条如图交叉,请判断重叠部分是一个什么图形?并证明你的结论。
(2) 若两张矩形纸条的长度均为8,宽度均为2,请求出重叠部分的图形的周长的最大值。
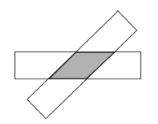
【答案】(1)菱形;(2)周长为17
【解析】
(1)首先可判断重叠部分为平行四边形,且两条纸条宽度相同;再由平行四边形的面积可得邻边相等,则重叠部分为菱形.(2)画出图形,设菱形的边长为x,根据勾股定理求出周长即可.
(1)过点A作AE⊥BC于E,AF⊥CD于F,
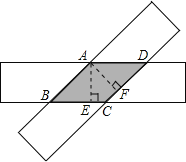
∵两条纸条宽度相同(对边平行),
∴AB∥CD,AD∥BC,AE=AF,
∴四边形ABCD是平行四边形,
∵SABCD=BCAE=CDAF,
又∵AE=AF,
∴BC=CD,
∴平行四边形ABCD是菱形;
(2)当两张纸条如图所示放置时,菱形周长最大,
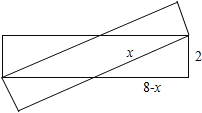
设这时菱形的边长为xcm,
由勾股定理可得,
![]() ,
,
解得x=![]() ,
,
∴菱形的周长为17.

练习册系列答案
相关题目