Question

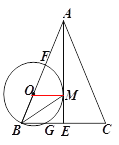
【题目】如图，△ABC内接于⊙O，AB=8，AC=4，D是AB边上一点，P是优弧的中点，连接PA，PB，PC，PD，当BD的长度为多少时，△PAD是以AD为底边的等腰三角形？并加以证明．

Answer 1

【答案】当BD=4时，△PAD是以AD为底边的等腰三角形．理由见解析.

【解析】

解：当BD=4时，△PAD是以AD为底边的等腰三角形。理由如下：

∵P是优弧的中点，∴。∴PB=PC。

若△PAD是以AD为底边的等腰三角形，则PA=PD。

又∵∠PAD=∠PCB，∴△PAD∽△PCB。∴∠DPA=∠BPC。∴∠BPD=∠CPA。

在△PBD与△PCA中，∵PB=PC，∠BPD=∠CPA，PD="PA" ，∴△PBD≌△PCA（SAS）。

∴BD=AC=4。

由于以上结论，反之也成立，

∴当BD=4时，△PAD是以AD为底边的等腰三角形。

根据等弧对等弦以及全等和相似三角形的判定与性质进行求解。