��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�A (16��0)��C (0��8)���ı���OABC�Ǿ��Σ�D��E�ֱ���OA��BC���ϵĵ㣬����DE�۵����Σ���Aǡ������y���ϵĵ�C������B���ڵ�B'����
(1) ��D��E��������ꣻ
(2) ����������y =![]() (k >0) �ڵ�һ����ͼ��E�㣬�ж�B���Ƿ������������������ͼ����? ��˵�����ɣ�
(k >0) �ڵ�һ����ͼ��E�㣬�ж�B���Ƿ������������������ͼ����? ��˵�����ɣ�
(3) ��F�� (2) �з�����������ͼ����ԭ���ε�AB�ߵĽ��㣬��G��ƽ��ֱ������ϵ�У��Ե�D��E��F��GΪ������ı�����ƽ���ı���,��G������꣮(ֱ��д����)

���𰸡���1��E��10��8����2�����ڣ���3��G1��20��13����G2��12��-3����G3��0��3��
�������������������1����OD=m����CD=DA=16-m����Rt��COD�У��ɹ��ɶ����ɵ�m=6�����ɵ�D�����꣬�ٸ��ݾ��ε����ʣ��ɵ�CE=CD=10���ɵ�E�����ꣻ
��2����B����B��M��BC��M����B��M��CM�ij��������ɵ�k��ֵ���������⣬�ɵô𰸣�
��3���������⣬������������ۣ��ɵ���ƽ��ֱ������ϵ�д���G1��G2��G3�����꣬�����ɵô𰸣�
�����������1��OA=16��OC=8��
��OD=m����CD=DA=16-m
��Rt��COD����COD=90��
��CD2=OC2+OD2
�ࣨ16-m��2=82+m2
���m=6��
��D��6��0��
���ı���OABC�Ǿ���
��OA��CB
���CED=��EDA
�ߡ�EDA=��CDE
���CED=��CDE
��CE=CD=10��E��10��8��
��2����ͼ����B����B��M��BC��M
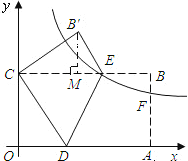
��B��C=AB=8��B��E=BE=6����CB��E=90��
��B��M=![]() ��B�䣨6.4��12.8��
��B�䣨6.4��12.8��
��k=10��8=80��y��![]()
�֡�6.4��12.8��80
���B�䲻�����������������ͼ����
��3����x=16ʱ��y=5
��F��16��5��
�����������ͼ��
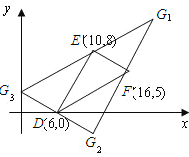
�ٰ��߶�DE������ƽ��10����λ���ȣ�������ƽ��5����λ���˵�E����G1����G1��20��13����
�ڰ��߶�EF������ƽ��4����λ���ȣ�������ƽ��8����λ���˵�F����G2����G2��12��-3����
�۰��߶�DF������ƽ��6����λ���ȣ�������ƽ��3����λ���˵�D����G3����G3��0��3����
������������ƽ��ֱ������ϵ�д���G1��20��13����G2��12��-3����G3��0��3��ʹ���Ե�D��E��F��GΪ������ı�����ƽ���ı��Σ�

 ���ٴ�����ɽ����ϵ�д�
���ٴ�����ɽ����ϵ�д� ���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
